20 дней и 30 дней.
Объяснение:
Пусть один из сварщиков может выполнить всю работу за х дней,
тогда другой сварщик - за (25 * 2 - х) дней или (50 - х) дней.
Примем всю работу за 1, тогда производительность труда у первого сварщика равна 1/х, у второго сварщика - 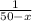 .
.
Совместна производительность труда двух сварщиков равна:
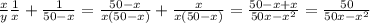
Составим уравнение и решим его:
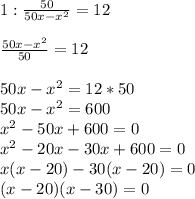
1) x - 20 = 0
x = 20 (дней)
2) x - 30 = 0
x = 30 (дней)
Допустим, что один из сварщиков может выполнить всю работу за 20 дней, тогда второй сварщик может выполнить всю работу за:
50 - 20 = 30 (дней) и наоборот.
См. рисунок в приложении.
а) На отрезке [π/6; 2·π/3] функция y=cosx убывает, поэтому:
наибольшего значения достигает в левой границе, то есть при x = π/6: y(π/6)=√3/2;наименьшего значения достигает в правой границе, то есть при x = 2·π/3: y(2·π/3) = -1/2б) интервал (-π; π/4) содержит значения x=-π и x = 0, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = -π: y(-π) = -1;в) луч [-π/3; +∞) содержит значения x=0 и x = π, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = π: y(π) = -1;г) полуинтервал [-π/3; 3π/2) содержит значения x=0 и x = π, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = π: y(π) = -1.![Найдите наименьшее и наибольшее значение функции y=cosx а) на отрезке [π/6; 2π/3] б) на интервале (-](/tpl/images/0936/5711/c9260.jpg)
p=0.4
1.9x0.4+2=2.76