Сэлектромотора за 7с можно накачать в бак 20 л воды. а) за какое время можно наполнить бак , вмещающий 200 л воды ? 120 л воды ? б) сколько воды можно накачать в бак за 14 с ? за 35 с ?

👇

Увидеть ответ

Ответ:

taisiachervatuk

23.04.2023

А)200/20х7=70,120/20х7=42 />б) 14/7х20=40 л,35/7х20=100 л

4,8(91 оценок)

Открыть все ответы

Ответ:

Bublick08

23.04.2023

просто подряд подставлять целые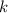

при 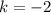k=-2 имеем корни

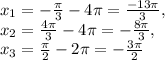
$x_1=-\frac{\pi}{3}-4\pi=\frac{-13\pi}{3},\\x_2=\frac{4\pi}{3}-4\pi=-\frac{8\pi}{3},\\x_3=\frac{\pi}{2}-2\pi=-\frac{3\pi}{2}$

Первые два в промежуток не попадают, третий - попадает.

при 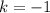k=-1 имеем корни

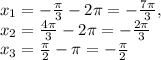$x_1=-\frac{\pi}{3}-2\pi=-\frac{7\pi}{3},\\x_2=\frac{4\pi}{3}-2\pi=-\frac{2\pi}{3}\\x_3=\frac{\pi}{2}-\pi=-\frac{\pi}{2}$ ,

первый корень в промежуток не попадает, другие два - попадают.

Если подставлять 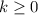$k\geq 0$ , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.

универсальный, но не очень удобный): оценить и проверить, при каких целых 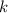неравенство 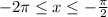$-2\pi\leq x\leq -\frac{\pi}{2}$ имеет решение. Для этого все серии корней по отдельности подставляем вместо :

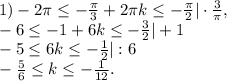
$1) -2\pi\leq -\frac{\pi}{3}+2\pi k\leq -\frac{\pi}{2} |\cdot\frac{3}{\pi} ,\\-6\leq -1+6k \leq -\frac{3}{2}|+1\\-5\leq 6k\leq -\frac{1}{2} |:6\\-\frac{5}{6}\leq k\leq -\frac{1}{12}.$

Очевидно, что целых 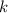, удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.

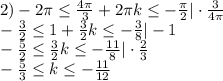
$2) -2\pi\leq \frac{4\pi}{3}+2\pi k \leq -\frac{\pi}{2}|\cdot\frac{3}{4\pi}\\ -\frac{3}{2} \leq 1+\frac{3}{2}k\leq -\frac{3}{8}|-1\\-\frac{5}{2}\leq \frac{3}{2}k\leq -\frac{11}{8}|\cdot\frac{2}{3}\\-\frac{5}{3}\leq k\leq -\frac{11}{12}$

Последнему неравенству удовлетворяет только одно целое 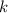- 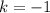k=-1 . Корень находим при подстановке значения 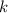в соответствующую серию.

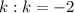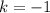То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения k: k=-2 и k=-1 . Их также подставляем в соответствующую серию и находим корни.

4,6(50 оценок)

Ответ:

макс190

23.04.2023

Пусть x - время которое мы потратили на встречу, тогда (х-10) - время которое ушло у деда на встречу. (100×x) - расстояние которое мы проехали. (50×(x-10)) - расстояние которое проехал дед.
так как расстояние между друг доугом 4000 км, то состовим и решим уравнение
100×х+50×(x-10)=4000
раскроем скобки
100x+50х-500=4000
перенесем неизвествое влево, а известное вправо и сложем подобные слогаемые
150х=4500
х=30 (ч) - время которое мы потратили на вствечу
2) 30-10=20 (ч) - время которое потратил дед
3) 20+30=50(ч)
ОТВЕТ: всего навствечу друг другу мы ехали 50 часов

4,6(20 оценок)

Это интересно:

Транспорт

29.01.2023

Как найти верхнюю мертвую точку вашего двигателя (ВМТ)...

Образование-и-коммуникации

19.01.2021

5 простых способов запомнить математические и физические формулы...

Стиль-и-уход-за-собой

17.06.2020

Как сделать ретро шляпку с вуалью...

Компьютеры-и-электроника