Вычислить значение выражения а) 0,4у + 1 при у = -0,5 и 8 б) -5х-6*(9-2х) при х=6

👇

Ответ:

sofialipnitscka

08.08.2021

А) Если у= -0,5 и 8, то 0,4у+ 1
0,4у+ 1= - 0,5· 4+ 1= -2+ 1= -1
0,4у+ 1= 8· 0,4+ 1= 3,2 + 1= 4,2
б)Если х=6, то -5х- 6(9- 2х)= -5·6- 6·(9- 2·6)= -30- 6· (-3)= -30+ 18= -12

4,6(55 оценок)

Открыть все ответы

Ответ:

pashkevich00

08.08.2021

Два натуральных числа 16; 24.

Объяснение:

Найти два натуральных числа по заданным условиям.

Пусть первое число равно x, а второе равно y.

Тогда сумма их квадратов: x² + y² = 832,

а их произведение xy = 384.

Чтобы найти эти числа, решим систему уравнений.

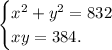
$\displaystyle \begin{cases} x^2 + y^2 = 832 \\ xy=384 . \end{cases}$

Умножим обе части второго уравнения системы на 2.

$\displaystyle \begin{cases} x^2 + y^2 = 832 \\ xy=384 \;\;|\cdot 2 \end{cases}; \;\;\; \; \displaystyle \begin{cases} x^2 + y^2 = 832 \\ 2xy=768 \end{cases}$

Сложим оба уравнения системы:

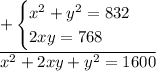
$\displaystyle +\begin{cases}x^2 + y^2 = 832\\2xy=768 \end{cases} \\\displaystyle \overline{x^2 +2xy+ y^2 = 1600}$

Свернем левую часть уравнения по формуле квадрата суммы двух выражений:

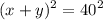
$\displaystyle (x+y)^2 = 40^{2}$

Получим следующую систему уравнений:

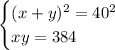
$\displaystyle \begin{cases} (x+y)^2 = 40^{2} \\ xy=384 \end{cases}$

Извлечем квадратный корень из обеих частей первого уравнения.

С учетом того, что нам даны натуральные числа, получим следующую систему уравнений:

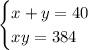
$\displaystyle \begin{cases} x+y = 40 \\ xy=384 \end{cases}$

Выразим переменную y через x в первом уравнении и подставим полученное выражение во второе уравнение.

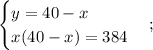
$\displaystyle \begin{cases} y = 40 -x\\ x(40-x)=384 \end{cases};$

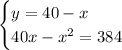
$\displaystyle \begin{cases} y = 40 -x\\ 40x -x^2=384 \end{cases}$

Решим второе уравнение системы.

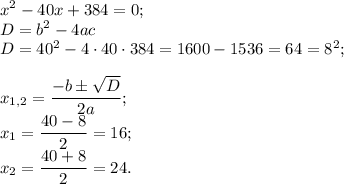
$\displaystyle x^2 -40x +384 = 0;\\\displaystyle D = b^{2} - 4ac \\D= 40^{2} -4\cdot 40 \cdot 384 =1600-1536=64=8^2;\\\\\displaystyle x_{1,2} =\frac{-b\pm\sqrt{D} }{2a};\\\displaystyle x_{1} =\frac{40-8}{2}=16;\\\displaystyle x_{2} =\frac{40+8}{2}=24.$

Тогда

$\displaystyle \begin{cases} x_{1}=16\\y_{1} = 40-16 \end{cases};\;\;\;\displaystyle \begin{cases} x_{1}=16\\y_{1} = 24 \end{cases};\\\\\displaystyle \begin{cases} x_{2}=24\\y_{2} = 40-24 \end{cases};\;\;\;\displaystyle \begin{cases} x_{2}=24\\y_{2}=16 \end{cases}$

Заданные натуральные числа 16 и 24.

4,7(79 оценок)

Ответ:

Рожок400000

08.08.2021

Чтобы найти вероятность, нужно количество благоприятных событий разделить на количество всех возможных событий.

Игральный кубик имеет 6 граней, значит при его бросании может выпасть либо 1, либо 2, либо 3, либо 4, либо 5, либо 6 - то есть количество всех возможных событий = 6.

По условию нам нужны только четные числа. В диапазоне от 1 до 6 всего 3 четных числа - 2, 4, 6, значит, количество благоприятных событий = 3.

Итак, количество благоприятных событий - 3, общее количество всех возможных событий - 6.

В числитель записываем благоприятные события (3), в знаменатель - все возможные события (6).

Найдем вероятность.

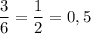$\displaystyle \frac{3}{6}=\frac{1}{2}=0,5$ - вероятность того, что при бросании кубика Ире выпадет четное число очков.