1,6x−2,5=4,1x
1.6х-4.1х=2.5
-2.5х=2.5
х=-1
-2x−20=7x+43
-2х-7х=43+20
-9х=63
х=-7
−16−1,5x=43,8+3,1x
-1.5х-3.1х=43.8+16
-4.6х=59.8
х=-13
0,9+7+(-6,53k)=12+0,9−6,73k
0.9+7-6.53k=12+0.9-6.73k
-6.53k+6.73k=12+0.9-0.9-7
0.2x=5
x=25
7⋅(7+y)−4y=4y−67
49+7у-4у=4у-67
7у-4у-4у=-67-49
-у=-116
у=116
Пусть рабочий изготовлена Х деталей в день. Тогда он их должен был изготовить за 360/Х дней.
Реально он делал х+20 деталей в день и по условию это заняло на 1,5 дня меньше
\begin{gathered}\frac{360}{x} - \frac{360}{x+20} =1,5 \\ \frac{360(x+20)-360x}{x(x+20)} =1,5 \\ \frac{360x+ 7200 - 360x}{x(x+20)} =1,5 \\ 7200=1,5x (x+20) \\ x^{2} +20x-4800=0 \\\end{gathered}
x
360
−
x+20
360
=1,5
x(x+20)
360(x+20)−360x
=1,5
x(x+20)
360x+7200−360x
=1,5
7200=1,5x(x+20)
x
2
+20x−4800=0
По теореме Винта
х1=-80
Х2=60
ответ: 60.
Пусть функция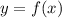 
возрастает на всей области определения.
Предположим, что для некоторых значений аргумента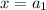 
и 
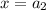выполняется соотношение 
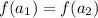. Рассмотрим три ситуации:
1. 
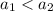- но по определению возрастающей функции меньшему значению аргумента соответствует меньшее значение функции: 
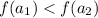- противоречие вышеприведенному равенству значений функции
2. 
- две точки равны между собой, значит и значения функции в них также равны, вышеприведенное равенство выполняется
3. 
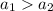- аналогично, по определению возрастающей функции большему значению аргумента соответствует большее значение функции: 
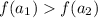- противоречие вышеприведенному равенству значений функции
Таким образом, при любых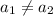 
не может выполняться равенство 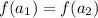. Это означает, что возрастающая функция не может принимать одно и то же значение в двух различных точках. Или по другому, возрастающая функция принимает каждое свое значение только в одной точке.
Для убывающей функции доказательство аналогичное с той лишь разницей, что случаю 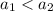соответствует условие 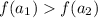, а случаю 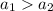- условие 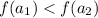. Но опять же, разным значениям аргумента не могут соответствовать равные значения функции.
1). 1,6x - 2,5 = 4,1x 2). -2x - 20 = 7x + 43
4,1x - 1,6x = -2,5 7x + 2x = -20 - 43
2,5x = -2,5 9x = -63
x = -1 x = -7
3). -16 -1,5x = 43,8 + 3,1x 5). 7·(7 + y) - 4y = 4y - 67
3,1x + 1,5x = -16 - 43,8 7y - 4y - 4y = -67 - 49
4,6x = -59,8 -y = -116
x = -13 y = 116
4). 0,9 + 7 + (-6,53k) = 12 + 0,9 - 6,73k
6,73k - 6,53k = 12,9 - 7,9
0,2k = 5
k = 25