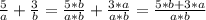
Объяснение:
Нам требуется привести две дроби к общему знаменателю и упростить, сложив их.
Как видно из знаменателя по правую сторону от знака "=", общим знаменателем двух дробей, будет являться их произведение, и чтобы привести две дроби к общему знаменателю, требуется числитель и знаменатель каждой дроби умножить на знаменатель другой дроби, то есть, наглядно это выглядит так:

Поэтому возвращаясь к нашему примеру, числитель и знаменатель первой дроби умножим на дробь 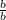 :
:

А числитель и знаменатель второй дроби на дробь 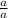 :
:
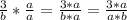
И теперь, так как наши дроби имеют одинаковые знаменатели, мы имеем право записать их под один общий знаменатель, который указан у Вас в правой части от знака "=":

Это и будет ответ на Ваше задание.
Пусть Х1, Х2 ... Xn - выборка независимых случайных величин.
Упорядочим эти величины по возрастанию, иными словами, построим вариационный ряд:
Х(1) < Х(2) < ... < X (n) , (*)
где Х(1) = min ( Х1, Х2 ... Xn),
Х(n) = max ( Х1, Х2 ... Xn).
Элементы вариационного ряда (*) называются порядковыми статистиками.
Величины d(i) = X(i+1) - X(i) называются спейсингами или расстояниями между порядковыми статистиками.
Размахом выборки называется величина
R = X(n) - X(1)
Иными словами, размах это расстояние между максимальным и минимальным членом вариационного ряда.
Выборочное среднее равно: = (Х1 + Х2 + ... + Xn) /