пусть Х-дней работает один 1-й, тогда (Х+10)дней работает один 2-й.
значит 1/х - это скорость работы в день 1-го, а 1/(х+10) - скорость работы 2-го. вместе они работали 12 дней, следовательно получаем уравнение
12/х +12/(х+10) = 1 привидем к общему знаменателю х(х+10) и оставим одни числители:
12х+12(х+10)=х(х+10)
12х+12х+120=х^2+10x
x^2-14x-120=0
D=676
x1=-6 - это отрицательное значение , чего быть не может при нашем условии
x2=20 -дней работал 1-й, 20+10=30-дней работаль 2-й.
1. y= (1/x) + 34
2.(не уверен, но вроде) y=∛(1-х^3 )
3. да
Объяснение:
1. как делается обратная функция: мы выражаем х через у, а потом в получившейся формуле меняем х на у
х-34=1/у
х=(1/у)+34
у=(1/х)+34
2. у^3=1-х^3
х^3=1-у^3
у=∛(1-х^3 )
3. что мы сделаем: мы возьмём произвольные х1 и х2, такие что х1>х2
и приведем к виду функции, если окажется, что выражение с х1 остается большим значит функция увеличивается, нет - наоборот.(не уверен в
х1>х2
-7х1<-7х2
10-7х1<10-7х2
выражение с х2 больше значит функция уменьшается, ответ да.
таким образом
согласно этим данным составим и решим уравнение:
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
не подходит по смыслу или не удовлетворяет условию, так как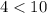
следовательно
х=30 (дней) - выкопает котлован второй экскаватор.
х-10=30-10=20 (дней) - выкопает котлован первый экскаватор Предположим, что х - время одиночной работы первого экскаватора, у - время одиночной работы второго экскаватора
таким образом
согласно этим данным составим систему уравнений и решим её:
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
не удовлетворяет условию, так как отрицательные дни быть не могут
следовательно
х=20 (дней) - выкопает котлован первый экскаватор.
y=x+10=20+10=30 (дней) - выкопает котлован второй экскаватор.
ответ: первый экскаватор выкопает котлован за 20 дней; второй экскаватор выкопает котлован за 30 дней.