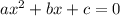
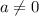, так как уравнение обращается в линейное.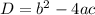
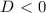уравнение не имеет решений (вообще имеет, но это в школе не проходят).
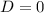то уравнение имеет 1 решение (корень).
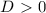- уравнение имеет 2 корня.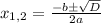
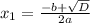
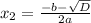
Приклад:
Розв'язати систему рівнянь: {x−2y=3,5x+y=4.
1) З першого рівняння системи виражаємо змінну x через змінну y.
Отримуємо: x−2y=3,x=3+2y;
2) Підставимо отриманий вираз замість змінної x у друге рівняння системи:
5⋅x+y=4,5⋅(3+2y)+y=4;
3) Розв'яжемо утворене рівняння з однією змінною, знайдемо y:
5⋅(3+2y)+y=4,15+10y+y=4,10y+y=4−15,11y=−11,|:11y=−1¯¯¯¯¯¯¯¯¯¯¯.
4) Знайдемо відповідне значення змінної x, підставивши значення змінної y, у вираз знайдений на першому кроці:
x=3+2⋅y,x=3+2⋅(−1),x=3−2,x=1¯¯¯¯¯¯¯¯.
5) Відповідь: (1;−1) .
Объяснение:
это решить линейные уравнения без черчежей
Координаты отрезка АВ:
АВ{Xb-Xa;Yb-Ya} или АВ{-3-(-6);5-9} или АВ{3;-4}
Длина (модуль) |AB|=√(3²+(-4)²)=√25=5.
Координаты середины М отрезка АВ:
Xm=(Xa+Xb)/2 или Xm=(-6+(-3))/2=-4,5.
Ym=(Ya+Yb)/2 или Ym=(9+5)/2=7.
М(-4,5;7).
ответ: АВ{3;-4}, |AB|=5. M(-4,5;7}.