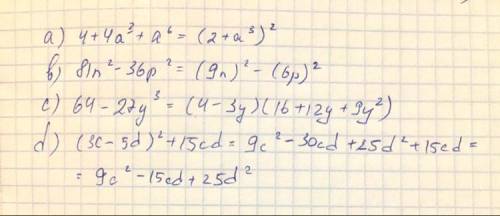
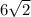Объяснение:1 Запишем
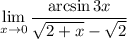2 Умножим на 1Но мы представим 1 как дробь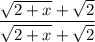 
, такое действие еще называют домножением на сопряжённое
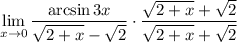
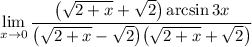
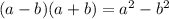где
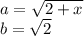
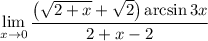
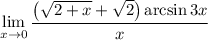
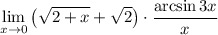7 Представим предел произведения как произведение пределов
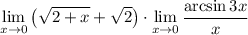8 Посчитаем первый предел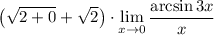
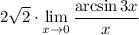9 Так как 
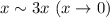то мы можем заметить в пределе 
на 
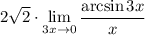10 Умножим выражение пол пределом на 1Но 1 мы представим в виде 
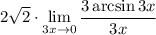
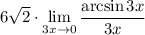
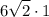ОТВЕТ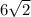
Задание №1.
1. На березе растут яблоки - Невозможное.
2. При бросании игральной кости выпала цифра 6 - Равновозможное.
3. За летом наступает осень - Достоверное.
Задание №2.
Всего двухзначных чисел у нас - 90 (от 10 до 99). Проще всего рещать в лоб, выбирая подходящие числа:
1) Нулём оканчивается каждое десятое из них, т.е. всего таких чисел 9. P = 9/90=0,1
2) Из одинаковых цифр состоит каждое одиннадцатое из них, начиная с 11, т.е. всего таких чисел 9. P = 9/90=0,1
3) Больше 27 и меньще 46 - всего 18 чисел, т.е. P =18/90=0,2
4) Квадратами целого числа являются 16, 25, 36, 49, 64, 81 - итого 6. P = 6/90=1/15
Задание №3.
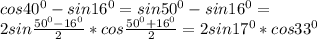
Объяснение:
