7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)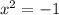 
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 
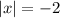
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)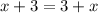 
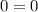
корней уравнения нет.
2) 
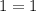
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: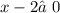 
, 
;
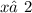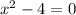
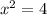
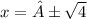
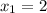(не удовлетворяет ОДЗ), 
ответ: 
2)
,
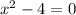
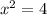
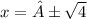
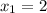ответ: ; 
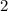
=> уравнения не равносильные.
10. 1)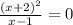 
ОДЗ: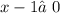 
, 
;
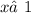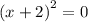
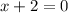
ответ:
2)
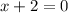
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 
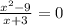
ОДЗ: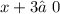 
, 
;
, 
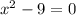
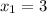(не удовлетворяет ОДЗ)
ответ: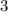 
13. 
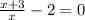
ОДЗ: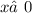 
;
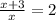
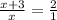
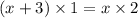
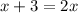
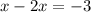
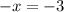
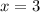
ответ: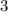
14. 
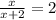
ОДЗ: 
, 
;
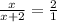
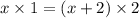
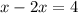
ответ: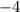 
15. 
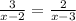
ОДЗ: , ,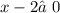 
, 
;
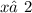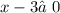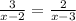
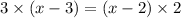
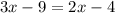
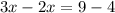
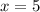
ответ: 
16. 
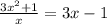
ОДЗ: ;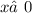
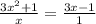
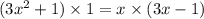
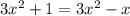
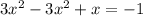
ответ: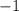 
Нули:
x = -8
x = 1
Знаки:
-8 1
- + -
ответ: x ∈ (-∞; -8) ∪ (1; +∞)