Графиком данной функции является парабола.
Область значения функции- это те числа, значение которых может принимать "y".
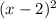означает, то что параболу 
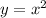сдвинули на две единицы измерения вправо относительно оси OY.
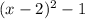означает то, что параболу 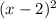сдвинули вниз на одну единицу измерения вниз относительно OX.
Исходя из это можно узнать, что координаты вершины стали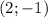 
Коэффициент "a" больше нуля, следовательно ветви параболы направлены вверх. А это значит, наименьшее значение функция будет принимать в вершине.
ответ: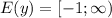 
Не может
Объяснение:
Всего единичных кубиков: p^3.
Из них кубиков, у которых не окрашено ни одной грани: (p-2)^3.
Это куб с ребром (p-2), который находится целиком внутри большого.
Посчитаем окрашенные кубики:
1) На вершинах 8 кубиков, у которых окрашено 3 грани.
2) На 12 ребрах 12(p-2) кубиков, у которых окрашено 2 грани.
3) На 6 гранях куба 6(p-2)^2 кубиков, у которых окрашена 1 грань.
И это количество должно быть равно неокрашенным кубикам.
(p-2)^3 = 6(p-2)^2 + 12(p-2) + 8
(p-2)^3 - 6(p-2)^2 - 12(p-2) - 8 = 0
Замена p-2 = t
t^3 - 6t^2 - 12t - 8 = 0
Так как t должно быть натуральным, то оно является делителем 8.
Пробуем 2, 4 и 8:
2^3 - 6*2^2 - 12*2 - 8 = 8 - 6*4 - 24 - 8 = -48
4^3 - 6*4^2 - 12*4 - 8 = 64 - 6*16 - 48 - 8 = -88
8^3 - 6*8^2 - 12*8 - 8 = 512 - 6*64 - 96 - 8 = 512 - 384 - 104 = 24
Ни одно из целых значений не подходит, значит, так сделать нельзя.
Попробуем на всякий случай 7:
7^3 - 6*7^2 - 12*7 - 8 = 343 - 6*49 - 84 - 8 = 343 - 294 - 92 = -43
t ∈ (7, 8), и оно иррациональное.
3х+15=-10-2х
3х+2х=-10-15
5х=-25
х=-5