1)постройте график функции y=x^2+4x-5 с таблицой. 2)укажите значения x,при которых y больше 0

👇

Ответ:

mardon1

02.10.2021

1) Таблица сданными и сам график, ниже

2) При Х< -5 и Х> 1 значение Y будет больше 0

1)постройте график функции y=x^2+4x-5 с таблицой. 2)укажите значения x,при которых y больше 0

1)постройте график функции y=x^2+4x-5 с таблицой. 2)укажите значения x,при которых y больше 0

4,8(21 оценок)

Открыть все ответы

Ответ:

olka11022000

02.10.2021

Для начала ОДЗ: x ≠ 96

Далее имеем два варианта:

(1) Либо, x - 96 > 0 (x > 96), тогда можем сократить знаменатели и получим x ≥ 1

(2) Либо, x - 96 < 0 (x < 96), тогда при сокращении знаменателя нужно будет перевернуть знак неравенства (т.к. сокращаем на отрицательное число). Получим x ≤ 1

Нас изначально интересует только 2 вариант, т.к. ищем отрицательные значения. В таком случае, x ∈ (-∞ ; 1]. Самым большим целым отрицательным числом на этом промежутке является единица ( -1 )

ответ: x = -1

Все. Будут вопросы - пиши :)

4,4(24 оценок)

Ответ:

kapitoshka202

02.10.2021

$p(x)=a_{1}x^4+a_{2}x^3+a_{3}x^2+a_{4}x+a_{5}\\
 x=\sqrt{x_{1}}\\
 x=\sqrt{x_{1}}+b\\
 x=\sqrt{x_{1}}+2b\\
 x=\sqrt{x_{1}}+3b\\\\
 p(x)+a=a_{1}x^4+a_{2}x^3+a_{3}x^2 + a_{4}x+a_{5}+a\\
y=\sqrt{y_{1}}\\
y=\sqrt{y_{2}}\\
y=\sqrt{y_{3}}\\
y=\sqrt{y_{4}}\\\\ 


$

По теореме Виета для уравнение четвертой степени получаем соотношение
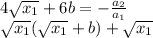
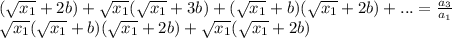
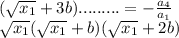
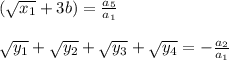
$4\sqrt{x_{1}}+6b = -\frac{a_{2}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)+\sqrt{x_{1}}$ $(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+3b)+(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+...=\frac{a_{3}}{a_{1}}\\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)+\sqrt{x_{1}}(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b).........=-\frac{a_{4}}{a_{1}} \\ \sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)$ $(\sqrt{x_{1}}+3b)=\frac{a_{5}}{a_{1}}\\\\ \sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}=-\frac{a_{2}}{a_{1}}\\$
\sqrt{y_{1}y_{2}}+\sqrt{y_{1}y_{3}}+\sqrt{y_{1}y_{4}}+\sqrt{y_{2}y_{3}}...+ = \frac{a_{3}}{a_{1}} \\ \sqrt{y_{1}y_{2}y_{3}}+\sqrt{y_{1}y_{2}y_{4}} [/tex]

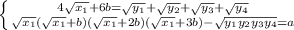
$\left \{ {{4\sqrt{x_{1}}+6b=\sqrt{y_{1}}+\sqrt{y_{2}}+\sqrt{y_{3}}+\sqrt{y_{4}}
 } \atop {\sqrt{x_{1}}(\sqrt{x_{1}}+b)(\sqrt{x_{1}}+2b)(\sqrt{x_{1}}+3b)-\sqrt{y_{1}y_{2}y_{3}y_{4}}=a} \right. \\
$
Учитывая условия что коэффициенты все выражаются в радикалах , то сумма всех корней выраженные в радикалах есть число радикальное .
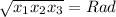По третьем равенству первой системы $\sqrt{x_{1}x_{2}x_{3}}=Rad$ , то произведение корней так же число радикальное , откуда с последних двух идет верное равенство