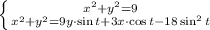
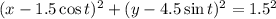, видим, что решениями системы есть координаты точек пересечений кругов с центрами 
и 
и 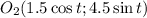радиусам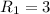и 
и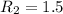 
согласно. Эти круги имеют единую общую точку в таких случаях
(внешний ощупь)
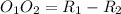(внутренний ощупь)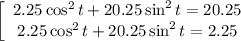
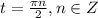. Остается при этих значениях параметра t решить систему уравнений.
решение системы будет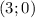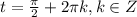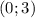 
решение системы: 
решение системы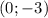 
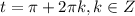, решение системы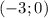 
пусть координаты центра какие то (x;y) и обозначим ее О ,
тогда ОМ1 = OM2 так как оба радиусы
OM1 =√(x-7)^2+(y-7)^2
OM2 = √(x+2)^2+(y-4)^2
корни можно убрать так как равны
(x-7)^2+(y-7)^2 = (x+2)^2+(y-4)^2
x^2-14x+49+y^2-14y+49 = x^2+4x+4 + y^2 - 8y + 16
-14x+49-14y+49=4x+4-8y+16
-18x- 6y = -78
теперь решаем это уравнение со вторым 2x-y-2=0 так как они имеют точки пересечения
{18x+6y=78
{2x-y=2
{y=2x-2
{ 18x+6(2x-2)= 78
18x+12x-12=78
30x = 90
x=3
y=4
то есть это и будут центры теперь найдем радиусы так
OM1 =R
R^2=(3-7)^2+(4-7)^2 = 16+9 = 25
и уравнение
(x-3)^2+(y-4)^2=25
x^2=5/2
x^2=2.5
x=+- √2.5
ответ: +-√2,5