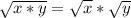
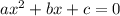, где коэффициент а не равен 0
Объяснение:
1 . 5) ( x + 1 )/(x²- xy ) i ( y - 1 )/(xy - y²) ;
y*(x + 1 )/xy(x - y ) i x*(y - 1)/xy(x - y ) ;
6) 6a/(a - 2b) i 3a/( a + b ) ;
6a( a + b )/(a + b)(a - 2b ) i 3a(a - 2b)/(a + b)(a - 2b ) ;
7) ( 1 + c²)/( c² - 16 ) i c/( 4 - c ) ;
( 1 + c²)/( c² - 16 ) i - c(c + 4 )/( c² - 16 ) ;
8) ( 2m + 9 )/(m² + 5m + 25 ) i m/(m - 5 ) ;
(2m + 9 )(m - 5)/(m - 5)(m²+5m +25 ) i m( m²+5m +25 )/(m - 5)(m²+5m +25 ).
Заметим, что если раскрывать скобки в выражении (a + b)^n, то получится (a^n + n a^(n - 1) b + ...) + b^n — разложение по биному Ньютона, где каждое слагаемое в скобках делится на a. Значит, (a + b)^n даёт такой же остаток при делении на a, что и b^n.
Используем это наблюдение. Представим выражение в виде (17 + 3)^n + (17 - 1)^n - 3^n - 1. По написанному выше это выражение даёт такой же остаток при делении на 17, что и 3^n + (-1)^n - 3^n - 1 = (-1)^n - 1. Для нечётных n последнее выражение равно -2, для чётных — 0. Значит, выражение делится на 17 при чётных n и не делится при нечётных.
Тот же трюк с делимостью на 19: (19 - 1)^n + (19 - 3)^n - 3^n - 1 ≡ (-1)^n + (-3)^n - 3^n - 1. Нечётные n нас уже не интересуют, а при чётных n последнее выражение равно 0, так что исходное выражение делится на n.
Суммируем: выражение делится на 323 при чётных n (и только при таких n). Значит, подходят n = 0, 2, 4, Седьмое число в этом ряду равно 12.
ответ. 12.