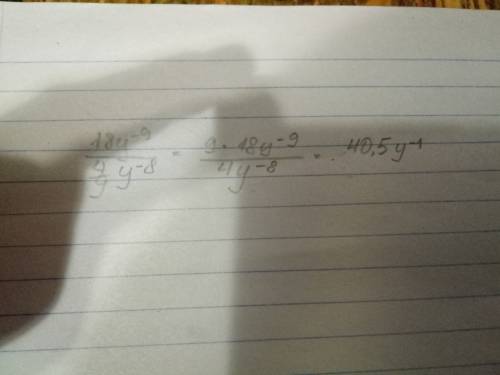
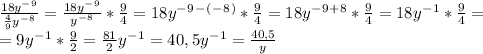
Объяснение:
1) Если количество домов N четное, то колодец можно поставить в любом месте между N/2 и (N/2 + 1) домом.
Например, если домов всего 2, то между 1 и 2 домами.
Обозначим S расстояние между домами.
Житель 1 дома пройдет до колодца расстояние x, а житель 2 дома расстояние S-x.
В сумме они пройдут x + S - x = S, то есть расстояние между домами.
Точно также, если домов 4, то колодец ставим между домами 2 и 3.
Тогда 1 и 4 жители вместе пройдут S, а 2 и 3 жители вместе пройдут s1 - расстояние между 2 и 3 домом.
Сумма равна S + s1.
Если же поставить колодец, например, между домами 1 и 2, то 2 житель пройдет расстояние y от 2 дома до колодца, а 3 житель (s1+y) - сначала s1 от 3 дома до 2, а потом ещё y до колодца.
В сумме получится
S + y + s1 + y = S + s1 + 2y > S + s1
Если же количество домов N нечетно, то ставить колодец надо во дворе среднего дома (N+1)/2.
Например, если домов 3, то ставим колодец около 2 дома.
Тогда для 1 и 3 жителя сумма расстояний будет по-прежнему S, а расстояние для 2 жителя будет 0.
Сумма всех расстояний равна S + 0 = S.
Точно также, для 5 домов колодец нужно ставить возле 3 дома, для 7 - возле 4, и т.д.
2) y = |x-a1| + |x-a2| + ... + |x-a(N)|
Это по сути та же задача.
y - сумма расстояний (модули - это расстояния между точками)
x - положение колодца
a1, a2, ... a(N) - положения домов.
И доказательство точно такое же.
Если N четно, то x может быть любым от a(N/2) до a((N+1)/2).
Если N нечетно, то x = a((N+1)/2)
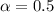 - вероятность победы
- вероятность победы
Иван и Алексей сыграют друг с другом в 1 туре, если так будет определено жеребьевкой.
Рассмотрим возможных соперников Ивана. Их 15 человек. Поэтому, вероятность того, что по результатам жеребьевки 1 тура Иван будет играть именно с Алексеем равна:
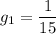
Таким образом, вероятность сыграть Ивану и Алексею в 1 туре между собой равна:
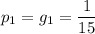
Если Иван и Алексей не сыграли между собой в 1 туре, то возможно они сыграют между собой во 2 туре. Но для этого каждому из них необходимо как минимум выиграть в 1 туре.
Вероятность того, что и Иван и Алексей окажутся во 2 туре, равна:
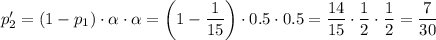
Во 2 туре играет 8 человек, то есть 7 возможных соперников для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:
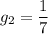
Значит, играть Иван и Алексей между собой во 2 туре будут с вероятностью:

Если Иван и Алексей не играли между собой во 2 туре, то они имеют шансы выйти в 3 тур. Это произойдет с вероятностью:

В 3 туре играет 4 человека, то есть 3 возможных соперника для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:
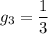
Значит, Иван и Алексей сыграют между собой в 3 туре с вероятностью:
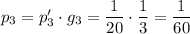
Вероятность выхода Ивана и Алексея в 4 тур:
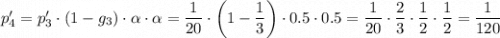
Если Иван и Алексей вышли в 4 тур, то есть в финал, то они, конечно, сыграют друг с другом:

Итоговая вероятность сыграть Ивану и Алексея друг с другом в каком-либо туре равна:
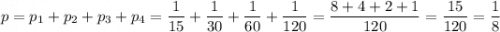
ответ: 1/8