![sin2x + 2sinx = 1 + cosx\\2sinxcosx+2sinx=1+cosx\\2sinx(1+cosx) = 1 + cosx\\(2sinx-1)(1+cosx) = 0\\sinx = \frac{1}{2} = x = (-1)^n\frac{\pi}{6} + \pi n, n \in Z\\ cosx = -1 = x = \pi + 2\pi m, m \in Z\\x \in [-4;-3]\\-4 < (-1)^n\frac{\pi}{6} + \pi n < -3\\-24 < (-1)^n\pi+6\pi n < -18\\](/tpl/images/1359/4064/d08e0.png)
Подставляем n = 0 - неравенство не выполнено. n = 1 - неравенство не выполнено. Следовательно, при n ≥ 0 решений не будет, т.к. (-1)^n + 6n - функция возрастающая.
Пусть n = -1, тогда выражение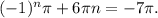 
Так как 3.14 < π < 3.15, то
-22.05 < -7π < -21.98. Очевидно, оно попадает на промежуток (-24; -18). Значит, при n = -1 решение есть на данном отрезке. Подставим n = -1 в серию корней:
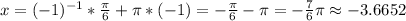
Такими же рассуждениями приходим к тому, что n ≤ -2 так же не являются решениями.
Теперь рассмотрим вторую серию корней:
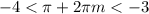
Тут совсем все просто: при m = 0, очевидно, неравенство не выполнено. При m = 1 так же. Так как выражение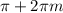 
при возрастании m увеличивается, то и m ≥ 2 также не подходят.
Пусть m = -1, тогда:
Очевидно, что это так. Подставляя m = -2 понимаем, что число меньше -4.
Вопросы ниже в комменты.
ответ: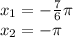 
a⁴+2a³b+2ab³+b⁴ ≥ 6a²b²
Перегруппируем члены:
a⁴+2ab*(a²+b²)+b⁴ -6a²b² ≥ 0
(a²+b²)²+2ab*(a²+b²)-4a²b² ≥ 0
(a²+b²)*(a²+b²+2ab)-4a²b² ≥ 0
(a²+b²)*(a+b)²-4a²b² ≥ 0
(a²+b²)*(a+b)² ≥ 4a²b²
Поскольку
(a-b)² ≥ 0 => a²+b² ≥ 2ab и
(a+b)² = a²+2ab+b² ≥ 2ab, то
(a²+b²)*(a+b)² ≥ 2ab*2ab ≥ 4a²b².