(1,2) -решение системы 1)
(-2, 3) -решение системы 2)
Объяснение:
при подстановке (х,у) оба равенства выполняются
1. Выпадение 2 очков при 1 бросании = 6, при втором бросании, тоже = 6, значит равновозможных исходов 6*6=36
2. Для того, чтобы 2 очка были наименьшими из выпавших, при первом броске должно выпасть 2, при втором броске - любое количество очков, кроме 1. Или при первом броске - любое, кроме 1, а при втором броске - 2 очка.
3. Возможен вариант выпадения 2 очков и при 1 и при 2 броске, поэтому, при подсчете, вариант это учитывается 2 раза.
3. Выпадение 2 очков из всех, кроме 1 очка = 5, при первом, и 5 при втором броске:
количество благоприятных исходов: 5+5-1=9 ((-1) - выпадение 2 очков в каждом из двух бросаний)
4. Вероятность благоприятного исхода: 9/36=1/4=0.25
ответ: 0.25
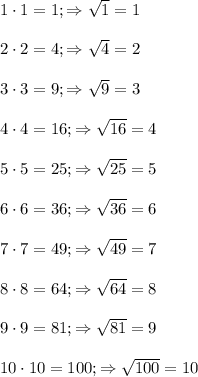
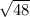и необходимо найти тот промежуток между целыми числами, которому принадлежит данное число. Смотрим в таблицу квадратов. Находим, что 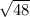находится между 
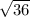и 
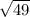, соответственно, 
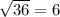, а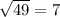 
. Таким образом, 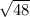лежит между целыми числам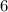и: 
и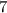 
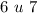
Объяснение:
Проверяем (-2;3)
1) (-2)²+3²=9
4+9≠9
пара не является решением
2) 2(-2)²-9+3=2 -(-2)²+2*3²=14
8-9+3=2 -4+18=14
2=2 14=14
пара является решением
Проверяем:
(1;2)
1) 1+2*4=9 3-5*2=-7
9=9 -7=-7
пара является решением
2) 2-4+2=2
0≠2
пара не является решением