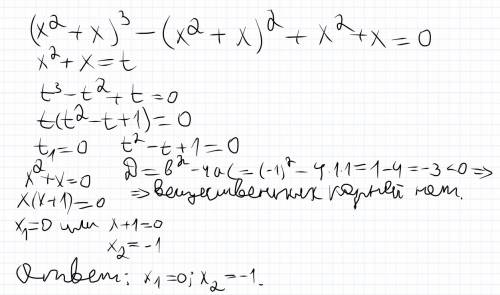
ответ:1) (5а+3)+(-3а-4)=5а+3-3а-4=2а-1
(5а+ 3)-(-3а-4)=5а+3+3а+4=8а+7
2) (7х2+3х)+(-2х-1)=7х2+3х-2х-1=7х2+ 1х-1
(7х2+3х)-(-2х-1)= 7х2+3х+2х+1=7х2+ 5х+1
3)( 8b2 + 2b - 4)+( 5 - 3b - 9b2)= 8b2 + 2b – 4+5 - 3b - 9b2=-b2-b+1
( 8b2 + 2b - 4)-( 5 - 3b - 9b2)= 8b2 + 2b – 4 -5+3b+9b2=17b2+ 5b-9
4) (11y - 12 - y3)+( 14 - 12y + y3)= 11y - 12 - y3+14 - 12y + y3=-y+y3+2
(11y - 12 - y3)-( 14 - 12y + y3)= 11y - 12 - y3-14+12y-y3=23y-2y3-26
5) (6 + mn + 2)+( 4 - mn - m2)= 6 + mn + 2+4 - mn - m2=12-mn-m2
(6 + mn + 2)-( 4 - mn - m2)= 6 + mn + 2-4+mn+m2=4+2mn+m2
Объяснение:
не благодарите
1) f(x)=1/(sin(x) - 0,5), т.к. функция y = 1/x определена на всем числовом промежутке, кроме x = 0, то и данная функция определена при всех x, кроме sin(x) - 0,5 = 0
sin(x) = 1/2
x = arcsin(1/2) + 2пn => x = п/6 + 2пn
x = п - arcsin(1/2) + 2пn => x = 5п/6 + 2пn
ответ: x ∈ R, x ≠ п/6 + 2пn, 5п/6 + 2пn, n ∈ Z
2)
а) y = 2sin(x ) - 3
Зная, что |sin(x)|≤ 1, то рассмотрим максимальное и минимальное значение функции:
y = 2 - 3 = -1
y = -2 - 3 = - 5
y = 0 - 3 = -3
ответ: y ∈ [-5; - 1]
б)y = 1 - cos(2x) = 1 - (cos^2(x) - sin^2(x)) = 1 - cos^2(x) + sin^2(x) = 2* sin^2(x)
y = 2 * 1^2 = 2
y = 2 * 0 = 0
ответ: y ∈ [0;2]
3)
а) y = x + cos(x), пусть x = -x
y = -x + cos(-x) = - x + cos(x)
- x + cos(x) ≠ x + cos(x) => ф-я нечетная
б) y = 3x^2 * sin x, пусть x = -x
y = 3 * (-x)^2 * sin(-x) = 3x^2 * (-sin(x)) = - 3x^2 * sin(x)
- 3x^2 * sin(x) ≠ 3x^2 * sin x => ф-я нечетная
y^3-y^2+y=0
y(y^2-y+1)=0
y=0
y^2-y+1=0
D=-3<0
x^2+x=0
x(x+1)=0
x=0
x+1=0
x=-1
ответ: 0; -1