Здесь есть несколько простых правил. Смотри:
1) 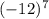 и
и 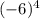
Есть правило о том, что любое число в чётной степени всегда 
То есть если мы (-6) возводим в чётную степень 4, то знак меняется с "минуса" на "плюс".
А вот с нечётной степенью это не работает. То есть если мы возводим (-12) в нечётную степень 7, то знак остаётся такой, какой был. А мы знаем, что любое отрицательное число всегда меньше положительного. Поэтому 
2) 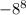 и
и 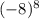
Здесь ещё проще. Под числом -8 мы понимаем -1*8. В первом случае (где без скобок записано) в восьмую степень возводится только сама 8, а "минус единица", можно сказать, остаётся за скобкой. Примитивно можем записать так:

Поэтому когда возводим 8 в восьмую (чётную) степень, знак всё равно не меняется, так как - 1 у нас осталось с таким же знаком "минус".
А вот во втором случае (где скобки) скобками нам показывают, что в чётную степень 8 возводиться как - 1, так и сама 8. Поэтому как ни крути, получим положительное число:

Значит, 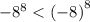
Тут одна параболf
когда квадратный трёхчлен записан в виде произведения то это означает:
ах²+bx+c= a(x-x₁)(x-x₂)- что тут указаны корни уравнения ах²+bx+c=0, то есть точки пересечения параболы с осью ОХ.
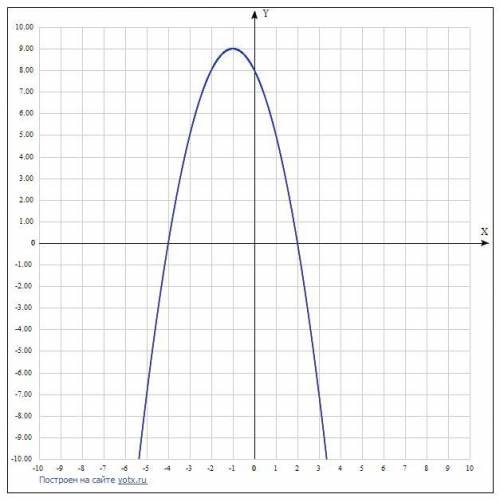
1)у= - (х-2)(х+4)- означает, что а<0 - ветви параболы направлены вниз,
2)точки с координатами (-4;0) и (2;0)- точки персечения графика с осью ОХ
3) легко найти ось симметрии она находится посередине между точками -4 и 2 , а акже параллельна оси ОУ
х= (-4+2):2= - 1 запишем отдельно:
х= -1
Для построения графика надо найти ординату вершины
уВ(-1)= - (-1-2)(-1+4) = - (-3)*3=9
координаты вершины (-1;9)
и найдём точку пересечения с осью ординат при х=0
у= - (0-2)(0+4)=8
точка пересечения с осью ОУ (0;8)
График в файле
проверка : -(х-2)(х+4)= - (х²+4х-2х-8)= - х²-2х+8
график и все тоски идентичны
x(y+z)
2(4c-5d)
ab(c-d)