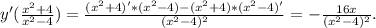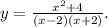1)x^2+9x+8 (x+1)(x+8) (x+8)
==
3x^2+8x+5 3(x+1)(x+1 2/3) 3x+5
x^2+9x+8=0 3x^2+8x+5=0
D= 8^2-4*3*5=64-60=4
x1+x2=-9| -8(+)-))2
x1,2=
|-8;-1 6
x1x2=8 | x1=-1 ; x2=-1 2/3
2)
a)x(x+3)-4(x-5)=7(x+4)-8
x^2+3x-4x+20=7x+28-8
x^2-8x=0
x(x-8)=0
x=0 или х-8=0
х=8
б)2x^4-9x+4=0
D=(-9)^2-4*2*4=81-32=49
9(+(-))7
x1,2=
4
x1=4; x2=0.5