1) -2 5 -7 1 0 0 2) С непосредственной подстановкой я думаю все ясно. А выполнить проверку с схемы Горнера можно найдя остаток от деления исходного многочлена на (x-x0) (ведь по теореме Безу и будет значением многочлена в точке x0). Схему Горнера тут неудобно оформлять, поэтому давай сам как нибудь. 3) В соответствии с теоремой о рациональных корнях многочлена с целыми коффициентами, целые корни должны быть делителями свободного члена 3. Делители тройки: 1, -1, 3, -3. Убеждаемся что только числа 1 и 3 являются корнями. ответ: x=1, x=3 4) Сначала поищем целые корни. Проверим числа 1, -1, 3, -3, 9, -9. 1 - корень, поэтому делим исходный многочлен на (x-1) и получаем 5x^2+14x+9. Теперь решаем квадратное уравнение находим еще два корня x=-9/5 и x=-1 Таким образом 5x^3+9x^2-5x-9=(x-1)(x+1)(5x+9)
Если многочлен имеет целые корни, то они явл. делителями свободного члена. В нашем случае своб. член = 8. Его делители: 1 , -1 , 2 , -2 , 4 , -4 , 8 , -8 . При подстановке х=1 в многочлен, он обращается в 0, поэтому х=1 - корень многочлена, а значит делится без остатка на (х-1).
По теореме косинусов
По теореме синусов
Площадь треугольника ABC: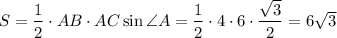 кв. ед.
кв. ед.
С другой стороны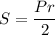 отсюда и выразим радиус вписанной окружности
отсюда и выразим радиус вписанной окружности