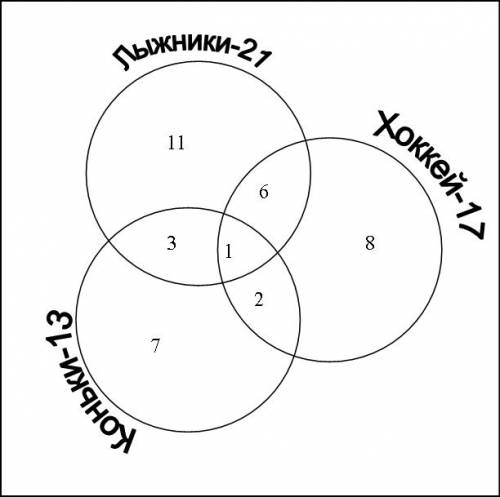
Всего на хоккей ходят 17 человек, из них 6 так же ходят на лыжи, 2 на коньки и 1 ходит и на коньки и на лыжи, а чисто хоккеистов 8.
Из всех лыжников 6 занимаются хоккеем
3-коньки
1 и лыжи и коньки
Т.е. 4 лыжников также занимаются коньками
Из коньков 5 занимаются двумя секциями: и из них уже известно, что 3 - лыжами, значит еще 2 - хоккеем
Т.о. из 13 коньков: 3 лыжников, 2 хоккеистов, 1 лыже-хоккеист и 7 чисто коньков
Значит всего тех, кто ходит на коньки, но при этом не ходит на лыжи 7+2=9 человек
В двух секциях будет 21+9=30 человек, значит чисто хоккеистов будет 38-30=8 человек
Прибавим к этим 8, еще 6-из лыжников, 2 коньков и 1 лыже-конька и получим 8+6+2+1=17
См. рисунок
Для решения неравенства методом интервалов будем выполнять следующие шаги
1) найдем корни уравнения уравнения
(x+3)(x-4)(x-6)=0
произведение равно нуля когда любой из множителей равен нулю
х+3=0 или х-4=0 или х-6=0
тогда х= -3 или х= 4 или х=6
2) Нарисуем числовую ось и отметив полученные точки
-3 4 6
3) в каждом из полученных промежутков определим знак нашего выражения
при х< -3 проверим для точки х= -5
(-5+3)(-5-4)(-5-6)=(-)(-)(-) <0
при -3<x<4 проверим для точки х=0
(0+3)(0-4)(0-6)=(+)(-)(-)>0
при 4<x<6 проверим для точки х=5
(5+3)(5-4)(5-6)=(+)(+)(-)<0
при x>6 проверим для точки х=10
(10+3)(10-4)(10-6)= (+)(+)(+)>0
4) расставим полученные знаки над промежутками
--3+4-6__+
5) и теперь осталось выбрать промежутки где стоит знак "минус"
( по условию <0)
Запишем полученные промежутки (-∞; -3) ∪(4;6)
где x больше или равно 0
-1/2x^4√(25x^2)=
=- ½x⁴•5x=-2,5x^5
b)6x^3√(4/x^2)
где x меньше нуля
6x^3√(4/x^2)=6x³•2/|x|=12х³/ |х|