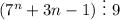
1 шаг. Проверим справедливость утверждения при n=1:
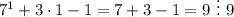 - верно
- верно
2 шаг. Предположим, что при n=k следующее утверждение верно:
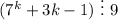
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
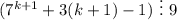
Для доказательства выполним преобразования:
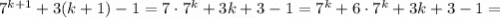
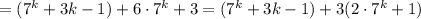
Рассмотрим получавшуюся сумму. Первое слагаемое 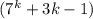 делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом
делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом 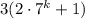 первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
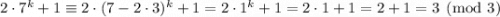
Мы получили, что выражение 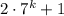 дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение
дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение 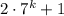 кратно 3.
кратно 3.
Возвращаясь к выражению 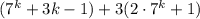 , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
, повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.