Теорема. Конечное объединение счетных множеств дает счетное множество.
По сути нужно доказать, что и и являются счетными. Докажем счетность множества .
Очевидно, что между каждым элементом множества можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество - счетно.
Докажем теперь счетность множества
Согласно основной теореме алгебры, полином -ой степени имеет различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество - счетно.
Пусть пешеход двигался со скоростью Х километров в час. Тогда скорость велосипедиста была Х+11 км/ч. За полчаса форы, которая была у пешехода, он успел пройти 0,5*Х км. Дальше до момента встречи велосипедист и пешеход двигались равное количество времени - положим, У часов. За это время велосипедист проехал (Х+11)*У км, а пешеход Х*У км. При этом общий путь пешехода составил 5 км, а путь велосипедиста - 13-5=8 км. Получаем систему из двух уравнений. Отрицательный корень противоречит смыслу задачи - отбрасываем. Следовательно, пешеход двигался со скоростью 5 км/ч, а велосипедист - 5+11=16 км/ч. Проверка. За первые полчаса пешеход км. Далее ему осталось пройти до точки встречи еще 2.5 км - и он их тоже за полчаса. В то же время за эти вторые полчаса велосипедист проехал 16/2=8 км - ровно то расстояние, что отделяло его от точки встречи. ответ: Велосипедист двигался со скоростью 16 км/ч.
Пусть пешеход двигался со скоростью Х километров в час. Тогда скорость велосипедиста была Х+11 км/ч. За полчаса форы, которая была у пешехода, он успел пройти 0,5*Х км. Дальше до момента встречи велосипедист и пешеход двигались равное количество времени - положим, У часов. За это время велосипедист проехал (Х+11)*У км, а пешеход Х*У км. При этом общий путь пешехода составил 5 км, а путь велосипедиста - 13-5=8 км. Получаем систему из двух уравнений. Отрицательный корень противоречит смыслу задачи - отбрасываем. Следовательно, пешеход двигался со скоростью 5 км/ч, а велосипедист - 5+11=16 км/ч. Проверка. За первые полчаса пешеход км. Далее ему осталось пройти до точки встречи еще 2.5 км - и он их тоже за полчаса. В то же время за эти вторые полчаса велосипедист проехал 16/2=8 км - ровно то расстояние, что отделяло его от точки встречи. ответ: Велосипедист двигался со скоростью 16 км/ч.
Теорема. Конечное объединение счетных множеств дает счетное множество.
По сути нужно доказать, что и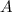 и
и 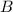 являются счетными. Докажем счетность множества
являются счетными. Докажем счетность множества 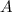 .
.
Очевидно, что между каждым элементом множества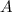 можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество
можно поставить взаимоднозначное соответствие с множеством натуральных чисел, которое как известно является счетными, т.е. множество 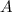 - счетно.
- счетно.
Докажем теперь счетность множества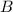
Согласно основной теореме алгебры, полином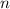 -ой степени имеет
-ой степени имеет 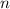 различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество
различных корней, т.е., очевидно, что количество полиномов является счетным, поскольку для каждого полинома можно установить биекцию множеству натуральных чисел, причем каждый полином имеет конечное число корней, тогда по выше сказанной теореме множество 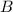 - счетно.
- счетно.
Следовательно,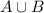 - счетно.
- счетно.