1) х₁=0, х₂=5, х₃=-5
2) х=1/12
3) х₁=3, х₂=4, х₃=-4.
Объяснение:
1) 4x³-100x = 0
Выносим общий множитель - 4х - за скобки.
4х(х²-25)=0
Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
4х=0
х=0
х²-25=0
х²=25
х=±√25
х=±5
ответ: х₁=0, х₂=5, х₃=-5.
2) 144x^3-24x^2+x=0
Выносим общий множитель - х - за скобки.
х(144х²-24х+1)=0
х=0
144х²-24х+1=0
Квадратное уравнение решаем через дискриминант.
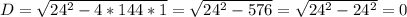
Уравнение будет иметь один корень, т.к. дискриминант равен нулю.
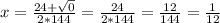
ответ: х=1/12.
3) x³-3x²-16x+48=0
Сгруппируем.
(х³-3х²)+(-16х+48)=0
Из первой скобки вынесем общий множитель х², а из второй (-16).
х²(х-3)-16(х-3)=0
Вынесем за скобки общий множитель (х-3).
(х-3)(х²-16)=0
х-3=0
х=3
х²-16=0
х²=16
х=±√16
х=±4
ответ: х₁=3, х₂=4, х₃=-4.
Відповідь:
y=1-2x
5x+2y=0 - в это уравнение нужно вместо y подставить 1-2x
5x+2(1-2x)=0 - ну и открываем скобки и считаем чему равен x
5x+2-4x=0
x=-2 - теперь возвращаемся к уравнению y=1-2x (вместо x подставляем -2)
y=1-2*(-2)
y=5
ответ (-2;5) - на первое место ставим значение икса
второе методом подстановки решить не получиться... только так
3x+2y=8 *(-3)
2x+6y=10
-9x-6y=-24
2x+6y=10
-9x-6y+2x+6y=-24+10
(-6y и6y сокращаются )
-9x+2x=-14
-7x=-14
x=2
подставляем X в уравнение
3*2+2y=8
6+2y=8
2y=8-6
2y=2
y=1
(2;1)
2х-3у=-8 |*(-5)
10x+4y=-2
-10x+15y=40
19y=38;
y=2
10x+4*2=-2;
10x=-10;
x=-1
ответ:
x=-1
y=2