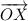, точку О будем считать началом координат. Т.е. мы получили ось ОХ, которая разбивает всю плоскость на верхнюю и нижнюю полуплоскости. Если в каждой полуплоскости лежит по 299 точек, то это и есть средняя линия. Если в верхней полуплоскости n точек, а в нижней m и, допустим, m<n, то повернем прямую ОХ вокруг точки О против часовой стрелки до тех пор, пока она первый раз не пройдет через другую точку ( допустим Y). В результате такого поворота, количество точек в каждой полуплоскости либо останется неизменным, либо уменьшится на 1, либо увеличится на 1. Это так, потому что никакие 3 точки не лежат на одной прямой. Причем, если в одной полуплоскости число точек увеличилось на 1, то во второй - уменьшилось на 1, т.к. общее количество точек 598 (не считая тех двух, через которые проходит прямая) остается неизменным. Это значит, что после такого поворота разность между количеством точек в верхней и нижней полуплоскости либо не изменилась, либо уменьшилась/увеличилась на 2.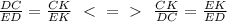 
Бурная, насыщенная жизнь Байрона была окружена ореолом романтики. О себе он писал: «…жил я не напрасно, хоть, может быть, под бременем невзгод, борьбою сломлен, рано я угасну, но нечто есть во мне, что не умрет, чего ни смерть, ни времени полет, ни клевета врагов не уничтожит…» И слова его оказались пророческими.
Родился Байрон в Лондоне 22 января 1788 года в аристократической семье. Отец его, женившийся во второй раз на девушке-шотландке, очень скоро промотал ее состояние и от кредиторов, скрылся во Франции, где спустя два года умер. Детство поэта в шотландском городке Эбердине. Жили они с матерью очень бедно. Чуткий ко всему красивому, мальчик полюбил суровую, но живописную природу тех мест, много читал, интересовался легендами о благородном разбойнике Робине Гуде, любил музыку.
Когда мечтательному, замкнутому Джорджу исполнилось десять лет, умер его двоюродный дед, оставив внуку родовое разрушенное имение Ньюстед в Ноттингемском графстве и титул лорда, который давал Байрону право по достижении совершеннолетия стать членом английского парламента. После первоначального обучения мальчик был отдан в аристократический колледж в Харроу (Гарроу). Здесь он оставил о себе память как справедливый и верный товарищ, любознательный, вдумчивый и вместе с тем живой юноша. Пытаясь исправить свой физический недостаток (хромоту), он серьезно занимался спортом, стал стрелком, боксером, наездником, отличным пловцом, но хромота его осталась. По окончании колледжа Байрон поступил в Кембриджский университет, где увлекался трудами французских просветителей и готовился к общественной и политической деятельности, для чего изучал риторику. Искусство оратора Байрон считал выше искусства поэта, хотя уже тогда писал стихи.
Изданный в 1807 году сборник его стихотворений «Часы досуга» носил следы подражания, но свидетельствовал о том, что у юного поэта крепнет собственный голос и формируется свое отношение к жизни. Чтобы это почувствовать, достаточно прочитать стихотворение «Хочу я быть ребенком вольным», в котором звучит грусть поэта о детстве и резкая критика жизни аристократической молодежи. Ему хотелось бы «снова жить в родных горах, скитаться по лесам раздольным, качаться на морских волнах…» Юноша тоскует по интересной, наполненной смыслом жизни: «Жить средь рабов - мне нет охоты, их руки пожимать - мне стыд!…» он был бы счастлив возвратить прежнее: