 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 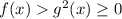 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 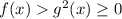 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
|-6|=6
V(пирамиды)=(1/3) V (параллелепипеда)=(1/3)·6=2