5 см и 12 см
Объяснение:
пусть стороны прямоугольника равны х и у (х,у>0).
тогда по условию:
х² + у² = 13²,х*у = 60.Решаем:
х² + у²=169,
ху=60;
х² + у²=169,
у=60/х;
х²+(60/х)²=169, (1)
у=60/х;. (2)
1. х² + 3600/х² = 169 |*х²
х⁴ + 3600 = 169х²
х⁴ - 169х² + 3600 = 0
пусть х²=t≥0
тогда t² - 169t +3600 = 0
D = (-169)² - 4*1*3600 = 28561 - 14400 =
= 14161 = 119²
t1 = (-(-169)+119) / (2*1) = (169+119)/2 = 288/2 = 144
t2 = (-(-169)-119) / (2*1) = (169-119)/2 = 50/2 = 25
выход из замены:
t=x², x>0
t1 = 144 = x², x1=√144 = 12,
t2 = 25 = x², x2=√25 = 5;
2. y=60/x
y1 = 60/x1 = 60/12=5
5y2 = 60/x2 = 60/5=12
То есть стороны прямоугольника: 5 и 12 см.
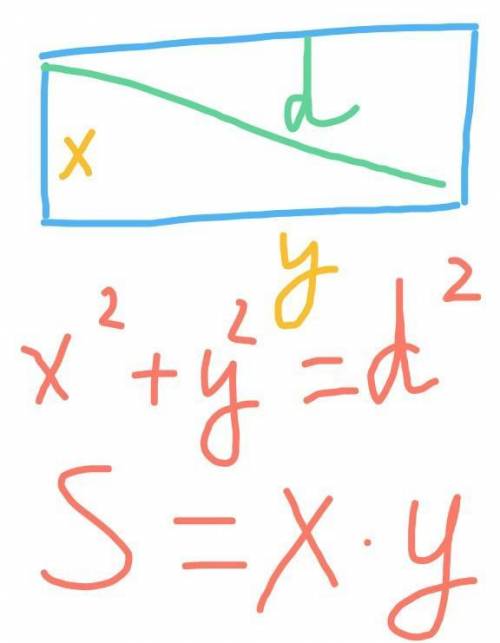
1.
a) P=P₁+P₂+P₃=0,15+0,25+0,4=0,8 вероятность попадания в 1 из 3-х областей
б) 1-Р=1-0,8=0,2 вероятность промазать (т.к. событие противоположное)
2.
Посчитаем от обратного.
Всего 6*6=36 возможных события
6 вариантов выпадения одинакового числа очков.
6/36 =1/6 вероятность выпадения одинакового числа очков.
Р=1-1/6=5/6 вероятность выпадения разного числа очков
3.
6*6=36 возможных событий
Выпадение очков меньше 3:
{1; 2}, {2; 1} - 2 варианта
Р=2/36=1/18 вероятность выпадения очков меньше 3-х
4.
6*6=36 событий
{6:6} - 1 событие выпадет 2 шестерки
Р=1/36 вероятность, что выпадет 2 шестерки
5.
Более 3-х очков: 4, 5, 6
Менее 3-х очков: 1,2,3
Р=3/6*3/6=1/4 вероятность, что на первой кости выпало
более трех очков, а на второй — менее трех
6.
Вероятность, что выпадет шестерка:
1/6
Вероятность, что выпадут 3 шестерки подряд:
Р=1/6*1/6*1/6=1/216