2 * cos ^ 3 x + 1 = cos ^ 2 (- 3 * п/2 - x);
2 * cos ^ 3 x + 1 = cos ^ 2 (- (3 * п/2 + x));
2 * cos ^ 3 x + 1 = cos ^ 2 (3 * п/2 + x);
2 * cos ^ 3 x + 1 = cos (3 * п/2 + x) * cos (3 * pi/2 + x);
2 * cos ^ 3 x + 1 = sin x * sin x;
2 * cos ^ 3 x + 1 - sin ^ 2 x = 0;
2 * cos ^ 3 x + sin ^ 2 x + cos ^ 2 x - sin ^ 2 x = 0;
2 * cos ^ 3 x + cos ^ 2 x = 0;
cos ^ 2 x * (2 * cos x + 1) = 0;
1) cos ^ 2 x = 0;
cos x = 0;
x = pi/2 + pi * n, где n принадлежит Z;
2) 2 * cos x + 1 = 0;
2 * cos x = - 1;
cos x = - 1/2;
x = + - arccos (-1/2) + 2 * pi * n, где n принадлежит Z;
x = + - 2 * pi/3 + 2 * pi * n, где n принадлежит Z;
ответ: x = pi/2 + pi * n и x = + - 2 * pi/3 + 2 * pi * n, где n принадлежит Z.
Объяснение:
Объяснение:
Мы докажем это равенство по индукции. Но сначала преобразуем правую часть равенства к более удобному для нас виду:
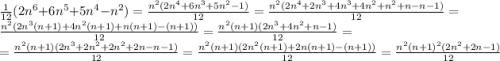А вот теперь применим индукцию. Легко проверить, что для n=1 равенство верно.
Теперь предположим что равенство верно для n=k:
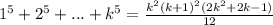
Прибавив к обеим частям равенства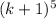 
получим:
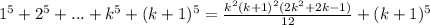
Займёмся преобразованием правой части этого равенства:
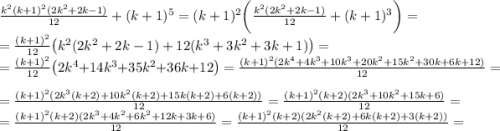
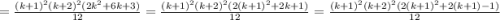Таким образом
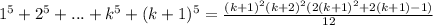
То есть если равенство верно для произвольного n=k, то оно также оказывается верным и для n=k+1. По индукции заключаем верность равенства для любого натурального n.
Если же вас интересует каким можно вывести формулу, которую мы только что доказали - напишите мне в ЛС.
ответ 2√3