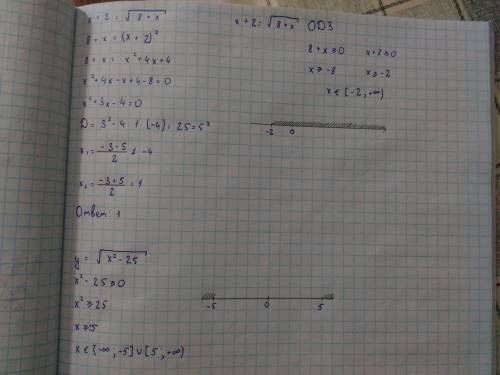
1) x∈(-∞; -5]∪[5; +∞); 2) x = 1
Объяснение:
у = √(x² - 25)
Подкоренное выражение должно быть неотрицательным
x² - 25 ≥ 0
(x - 5)(x + 5) ≥ 0
x ≤ -5 или x ≥ 5
Область определения: x∈(-∞; -5]∪[5; +∞)
x + 2 = √(8 + x)
равносильно системе
(x + 2)² = 8 + x и x + 2 ≥ 0; x ≥ -2
x² + 4x + 4 = 8 + x
x² + 3x - 4 = 0
x₁ = -4 - не подходит (должно быть x ≥ -2)
x₂ = 1 - подходит!
См. решение на рисунке

ответ:
начнем с 2-х-значных:
10х+у = 13х+13у, где х и у - натуральные числа от 1 до 9 и 0(для разряда единиц)
3х+12у = 0 - невыполнимо при натуральных х и у.
переходим к 3-х-значным:
100х + 10у + z = 13x + 13y + 13z
87x = 3y+12z
29x = y + 4z
видим, что х может быть равен только 1, так как при х> 1, правая часть не будет равняться левой ( максимально возможное значение правой части при у = z = 9 и равно 45)
итак получили: y+4z=29
для y,z - натуральных от 1 до 9, очевидно, что z может равняться только 5,6,7
тогда :
при z = 5, y =9
при z = 6, y = 5.
при z = 7, y = 1
итак получились числа: 195; 156; 117
для 4 и далее значных чисел рассмотрение теряет смысл, так как максимально возможная сумма цифр 4-значного числа равно 9*4 = 36. и если его умножить на 13 ника не получится 4-значное число..
ответ: 195; 156; 117.