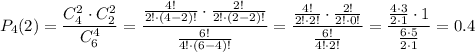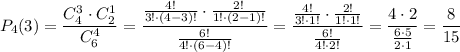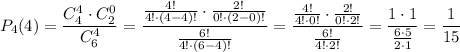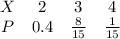За первую четверть по было задано 24 раза 1)ученик в 8 раз выполнил на оценку 5 какова абсолютная частота выполнения на оценку 5 ученика за четверть 2) ученика 12 раз выполнял на оценку четыре какова абсолютная частота выполнения на оценку четыре ученика за четверть 3) ученик 13 раз выполнял на оценку четыре какова абсолютная частота выполнения на оценку четыре отличную от 4

👇

Увидеть ответ

Ответ:

lililobanova20

05.06.2021

1) частота "5" 8/24 = 1/3 2) частота "4" 12/24 = 1/2 3) 13 раз на 4, и 24-13=11 раз не на 4. частота "не 4" 11/24.

4,4(28 оценок)

Открыть все ответы

Ответ:

nikitanehaenko1

05.06.2021

Для каждого задания нужно записать уравнение и решить его.

1) 3t + 5 = 5t + 13, 2) 3t + 17 = 2 · (5t - 5),

3t - 5t = 13 - 5, 3t + 17 = 10t - 10,

-2t = 8, 3t - 10t = - 10 - 17,

t = 8 : (-2) , -7t = -27,

t = -4 ; t = -27 : (-7),

t = 27/7 = 3 целых 6/7;

3) 3 · (3t - 11) = 5t - 17 , 4) (11 - 13t) - 7 = 8t + 11,

9t - 33 = 5t - 17, 4 - 13t = 8t + 11,

9t - 5t = -17 + 33 , -13t - 8t = 11 - 4,

4t = 16, -21t = 7,

t = 16 : 4, t = 7 : (-21),

t = 4 ; t = -1/3 ;

5) (0,5t + 3,1) + 8 = 0,5t - 4,9, 6) (81 - 8,3t) - (75 - 8,3t) = 3,

0,5t + 11,1 = 0,5t - 4,9, 81 - 8,3t - 75 + 8,3t = 3,

0,5t - 0,5t = - 4,9 - 11,1, 0t + 6 = 3,

0t = -16, 0t = 3 - 6,

нет решений; 0t = -3,

нет решений.

4,8(87 оценок)

Ответ:

modovonchik

05.06.2021

Так как всего учебников 6, их них 4 в переплете (то есть всего 2 учебника без переплета), то при выборе 4 учебников как минимум 2 из них будут в переплете. Следовательно, менее 2 учебников в переплете выбрать невозможно.

Найдем вероятность появления 2 учебников в переплете среди взятых:
- благоприятные исходы: произведение числа выбрать 2 учебника с переплетом из 4 и числа выбрать 2 учебника без переплета из 2:
- все возможные исходы: число выбрать 2 учебника из 6
Каждый выбор считаем сочетанием, так как порядок выбор не важен. Вероятность рассчитываем как отношение числа благоприятных исходов к общему числу всех возможных исходов:
$P_4(2)= \dfrac{C_4^2\cdot C_2^2}{C_6^4} = \dfrac{ \frac{4!}{2!\cdot(4-2)!} \cdot \frac{2!}{2!\cdot(2-2)!} }{ \frac{6!}{4!\cdot(6-4)!} } = \dfrac{ \frac{4!}{2!\cdot2!} \cdot \frac{2!}{2!\cdot0!} }{ \frac{6!}{4!\cdot2!} } = \dfrac{ \frac{4\cdot3}{2\cdot1} \cdot 1 }{ \frac{6\cdot5}{2\cdot1} } = 0.4$

Вероятность появления 3 учебников в переплете среди взятых: - благоприятные исходы: произведение числа выбрать 3 учебника с переплетом из 4 и числа выбрать 1 учебник без переплета из 2: - все возможные исходы: число выбрать 3 учебника из 6
$P_4(3)= \dfrac{C_4^3\cdot C_2^1}{C_6^4} = \dfrac{ \frac{4!}{3!\cdot(4-3)!} \cdot \frac{2!}{1!\cdot(2-1)!} }{ \frac{6!}{4!\cdot(6-4)!} } = \dfrac{ \frac{4!}{3!\cdot1!} \cdot \frac{2!}{1!\cdot1!} }{ \frac{6!}{4!\cdot2!} } = \dfrac{ 4 \cdot 2 }{ \frac{6\cdot5}{2\cdot1} } = \dfrac{8}{15}$

Вероятность появления 4 учебников в переплете среди взятых: - благоприятные исходы: произведение числа выбрать 4 учебника с переплетом из 4 и числа выбрать 0 учебников без переплета из 2: - все возможные исходы: число выбрать 4 учебника из 6
$P_4(4)= \dfrac{C_4^4\cdot C_2^0}{C_6^4} = \dfrac{ \frac{4!}{4!\cdot(4-4)!} \cdot \frac{2!}{0!\cdot(2-0)!} }{ \frac{6!}{4!\cdot(6-4)!} } = \dfrac{ \frac{4!}{4!\cdot0!} \cdot \frac{2!}{0!\cdot2!} }{ \frac{6!}{4!\cdot2!} } = \dfrac{ 1 \cdot 1 }{ \frac{6\cdot5}{2\cdot1} } = \dfrac{1}{15}$

Очевидно, что выбрать 5 и более учебников с переплетом невозможно.

Закон распределения имеет вид:
$\begin{array}{ccccc}X&2&3&4\\P&0.4& \frac{8}{15} & \frac{1}{15} \end{array}$