Произведение 3-х множителй делится на любой из своих множителей без остатка.
3*5*11=165 - минимальное 3-х значное число, делящееся на 3, 5 и 11.
Если это число умножить на любое число, это число все равно будет делиться на 3, 5 и 11, так как данные множители остаются и добавляется еще 1.
Ограничения: 3-х значное число и различные цифры. Значит, чтобы получить 3-х значное число, дополнительный множитель может быть не больше, чем 6:
165*6=990 - максимальное 3-х значное число, кратное 3, 5 и 11 одновременно.
Но, при умножении на четные числа от 2 до 6, получаем, соответственно, числа 330, 660 и 990, что выходит за рамки ограницения "различные цифры".
Значит, дополнительные множители, которые можно ввести, это - 3 и 5 (множитель 1 не вводится, потому, что произведение не изменится):
3*5*11*3=495
3*5*11*5=825
ответ: 165; 495; 825
22. -2
23. 1
Объяснение:
22. Рассмотрим каждое из подкоренных выражений:

Поскольку квадрат какого-либо числа неотрицателен, 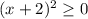 , отсюда:
, отсюда:

Значит, левая часть ![\sqrt[3]{2x^2+8x+72}+\sqrt[3]{3x^2+12x+12}\geq \sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/87f22.png)
Правая часть 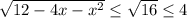
Левая часть не меньше 4, а правая не больше 4. Значит, равенство достигается тогда и только тогда, когда обе части равны 4. Правая часть равна 4:
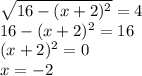
Проверим этот корень для левой части:
![\sqrt[3]{2(-2+2)^2+64}+\sqrt[3]{3(-2+2)^2}=\sqrt[3]{64}+\sqrt[3]{0}=4](/tpl/images/4540/3998/4cb78.png) — верно.
— верно.
Уравнение имеет единственный корень x = -2.
23. Заметим, что 
Значит, 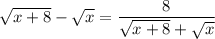 (знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит,
(знаменатель не обращается в ноль, так как x ≥ 0 по ОДЗ, значит, 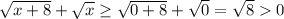 ).
).
Пусть  . Тогда уравнение имеет вид:
. Тогда уравнение имеет вид:
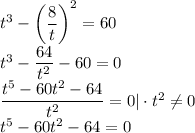
Заметим, что t = 4 — корень многочлена левой части. Поделив его столбиком на (t - 4), получим его разложение на множители:

Поскольку t > 0,  , значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:
, значит, обе части можно поделить на второй множитель, так как он не равен нулю. Получаем:

Левая часть неотрицательна, значит, правая часть также неотрицательна: 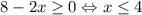
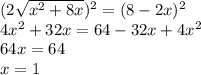
Корень удовлетворяет условиям 0 ≤ x ≤ 4, значит, он подходит.
1) g^3(в 3 степени)=c7/c4=25/корень из 5=корень из 125
g=5
2) g=1/3 : -1/9= -3
c4=c1*g3= -1/9 * (-3)^3(в 3 степени)=3
с5=c1*g4= -1/9 * (-3)^4(в 4 степени)= -9
с6=c1*g5= -1/9 * (-3)^5(в 5 степени)=27
P6(произв. 6 чл.)= (c1*c6*n)/2= (-1/9*27*6)/2= -9