См. рисунок
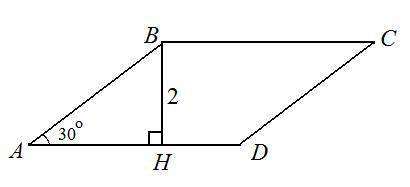
Пусть дан ромб АВСD, ВН ⊥ АD, ВН = 2, ∠ВАD = 30°. Найдем площадь ромба.
Т.к. ромб - это параллелограмм, у которого все стороны равны, то АВ = ВС = СD = АD и поэтому площадь ромба можно найти по формуле
S = ah, где a - сторона параллелограмма, h - высота параллелограмма, проведенная к этой стороне.
Значит, нужно найти сторону ромба. Для этого рассмотрим прямоугольный ΔАВН (ВН - высота, ∠ВАН = 30°). ВН - катет, лежащий против угла в 30°, а, значит, он равен половине гипотенузы, т.е. гипотенуза АВ = 2ВН = 4.
Таким образом, площадь ромба можно вычислить так:
S = АD · ВН = АВ · ВН = 4 · 2 = 8.
ответ: 8.
Объяснение:
2. Найди:
В четверти π/2 до π cos2<0
sin^2 a(альфа) = - √1 - 0.64 = - √0.36= - 0.6
Жауабы: cos a(альфа) = - 0.6
3. Вычислите:
2sin 15*cos15=sin 1\2(15+15)=1\2*1\2=1\4=0,25
4. Решите уравнение:
а) log2(2x-4)=7
2x-4=2^7
2x-4=128
2x=128+4
2x=132
x=66
2)log4 (x-2) + log1/2 (x-2) = 1/2
ОДЗ: х-2>0; х>2.
log2² (x-2) + log2^(-1) (x-2) = 1/2
1/2•log2 (x-2) - 1•log2 (x-2) = 1/2
-1/2•log2 (x-2) = 1/2
log2 (x-2) = 1/2 : (-1/2)
log2 (x-2) = -1
х-2 = 2^(-1)
х-2=1/2
х = 2 + 1/2
х = 2 1/2
2 1/2 входит в ОДЗ.
Жауабы: 2 1/2.