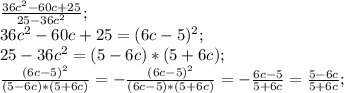
Числитель - сворачивается в квадрат разности, знаменатель - это разность квадратов.
Сворачивая по формуле квадрата разности числитель, и наоборот расписывая по разности квадратов знаменатель получаем вышесказаное выражение, далее, выносим минус за скобки, и в одной из скобок знаменателя меняем знак на противоположный, тем самым имеем право сократить с числителем. Далее, минус вносим в дробь, меняя знаки в числителе. Выходим на ответ.
Либо есть более короткий вариант решения, но тут нужна внимательность:
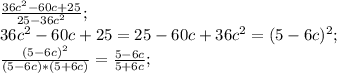
Т.к. это квадрат разности (В числителе) имеем право поменять местами 36c^2 и 25, сохраняя знаки. Свернется в тот-же самый квадрат разности, но нет заморочек с минусом.
fmin = -29, fmax = -11
Объяснение:
y = 2·x2+16·x+3
[-5;-1]
Необходимое условие экстремума функции одной переменной.
Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.
Достаточное условие экстремума функции одной переменной.
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) > 0
то точка x* является точкой локального (глобального) минимума функции.
Если в точке x* выполняется условие:
f'0(x*) = 0
f''0(x*) < 0
то точка x* - локальный (глобальный) максимум.
Решение.
Находим первую производную функции:
y' = 4·x+16
Приравниваем ее к нулю:
4·x+16 = 0
x1 = -4
Вычисляем значения функции на концах интервала
f(-4) = -29
f(-5) = -27
f(-1) = -11
fmin = -29, fmax = -11