1) Решение через дискриминант .
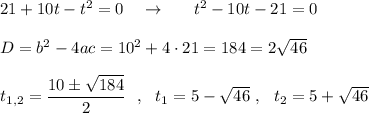
2) Решение с выделения полного квадрата .
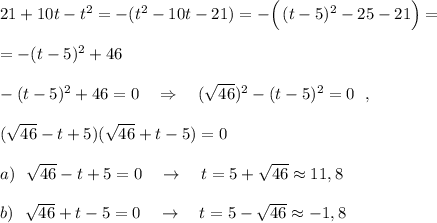
3) Решение с теоремы Виета.
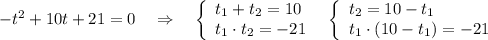
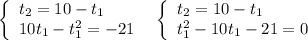
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения  .
.
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : 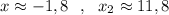 .
.
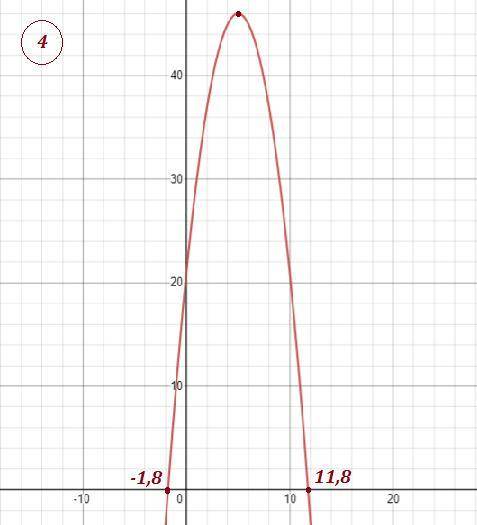
В решении.
Объяснение:
№1
Какая из следующих функций является квадратичной, ее выписать и указать ее коэффициенты:
а) у=х²+2-4х ; б) у=х²+22; в) у=-х-43х г) у=-3х²+27-5х; д) у=2-4х.
Квадратичные функции вида у = ax² + bx + c;
В квадратных уравнениях a называется первым коэффициентом (a ≠ 0), b называется вторым коэффициентом, c называется известным или свободным членом.
у=х²+2-4х; первый коэффициент = 1; второй = -4; свободный член = 2;
у=х²+22; первый коэффициент = 1; второй = 0; свободный член = 22;
у=-3х²+27-5х; первый коэффициент = -3; второй = -5; свободный член = 27.
№2
Найти координаты вершины параболы по формуле:
а) у = -х² + 2 - 4х;
б) у = х² + 22х - 3;
в) у = -х - 43х² + 5;
г) у = -3х² + 27 - 5х;
д) у = 12 - 4х².
Формула х₀ = -b/2a; потом значение х₀ подставить в уравнение функции и вычислить у₀. (х₀; у₀) - координаты вершины параболы.
а) у = -х² - 4х + 2;
х₀ = 4/-2
х₀ = -2;
у₀ = -(-2)² - 4 * (-2) + 2 = -4 + 8 + 2 = 6;
у₀ = 6;
Координаты вершины параболы: (-2; 6);
б) у = х² + 22х - 3;
х₀ = -22/2
х₀ = -11;
у₀ = (-11)² + 22 * (-11) - 3 = 121 - 242 - 3 = -124;
у₀ = -124;
Координаты вершины параболы: (-11; -124);
в) у = - 43х² - х + 5;
х₀ = 1/-86
х₀ = -0,01;
у₀ = -43 * (-0,01)² - (-0,01) + 5 = -0,0043 + 0,01 + 5 = 5,0057
у₀ = 5;
Координаты вершины параболы: (-0,01; 5);
г) у = -3х² - 5х + 27;
х₀ = 5/-6
х₀ = -5/6;
у₀ = -3 * (-5/6)² - 5 * (-5/6) + 27 = -25/12 + 25/6 + 27 = 349/12 = 29 1/12;
у₀ = 29 1/12;
Координаты вершины параболы: (-5/6; 29 1/12);
д) у = - 4х² + 12;
х₀ = 0/-8
х₀ = 0;
у₀ = -4 * 0² + 12
у₀ = 12;
Координаты вершины параболы: (0; 12),
№3
Составьте квадратный трехчлен ах²+вх+с, у которого:
а) а=3,в=-12,с=0; → 3х² - 12х;
б) а=1,в=0,с=4; → х² + 4;
в) а=-1,в=-1,с=114; → -х² - х + 114;
г)а=2,в=-1,с=0,5; → 2х² - х + 0,5;
д) а=-13,в=10,с=20; → -13х² + 10х + 20.
решаем это неравество:
определяем знаки на каждом промежутке:
на (-oo;-1)
берем -2: -8*(-1) - знак +
на (-1;6) берем 0: -6*1 - знак (-)
на (6;+oo) берем 7: 1*8 - знак +
решаем уравнение:
поочередно раскрываем модули:
1) 2x+1-(2x-3)-4=0, 2x+1>=0, 2x-3>=0
2x-2x+4-4=0
0x=0
x - любое число, но:
2x+1>=0
2x-3>=0
x>=-0,5
x>=1,5
значит промежутком решения является:
2)2x+1+2x-3-4=0, 2x+1>=0, 2x-3<=0
4x-6=0
4x=6
x=6/4=1,5
корень x=1,5 не подходит по изначальному одз
3)-2x-1-2x+3-4=0, 2x+1<=0, 2x-3>=0
-4x-2=0
4x=-2
x=-0,5 - не подходит по изначальному одз
4)-2x-1+2x-3-4=0, 2x+1<=0, 2x-3<=0
2x-2x-8=0
0x=8
x - нет решений
В итоге получили промежуток (6;+oo)
ответ: (6;+oo)