
с дискриминанта - 8 класс).
Решим квадратное уравнение через дискриминант. Если 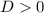 , то уравнение имеет 2 корня, если
, то уравнение имеет 2 корня, если 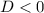 , то уравнение не имеет корней. (Если
, то уравнение не имеет корней. (Если 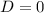 , то уравнение имеет 1 корень)
, то уравнение имеет 1 корень)
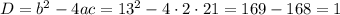
Поскольку 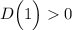 , то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.
, то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.
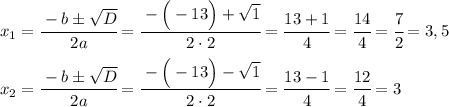
с группировки - 7 класс).
Представим число 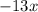 в виде двух чисел:
в виде двух чисел: 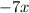 и
и 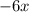 . А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.
. А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.
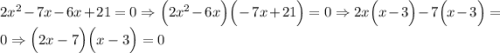
По правилу если произведение равно нулю, то хотя бы один из данных множителей будет равняться нулю. Рассмотрим 2 единственных случая.
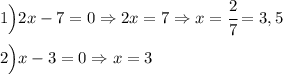
 .Задание #4.
.Задание #4.с дискриминанта - 8 класс).
Для начала нужно в правой части уравнения умножить многочлен на многочлен, а затем перенести все члены из правой части в левую со сменой знака, а в правой части поставим 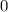 .
.
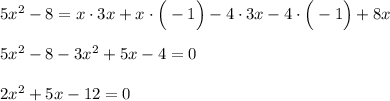
Найдём дискриминант данного квадратного уравнения. Если 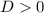 , то уравнение имеет 2 корня, если
, то уравнение имеет 2 корня, если 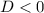 , то уравнение не имеет корней. (Если
, то уравнение не имеет корней. (Если 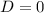 , то уравнение имеет 1 корень)
, то уравнение имеет 1 корень)
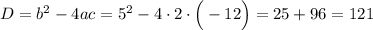
Поскольку 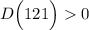 , то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.
, то данное квадратное уравнение имеет 2 корня. Найдём эти корни по формуле.
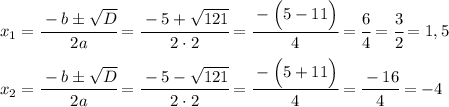
с группировки - 7 класс).
Представим число 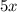 в виде двух чисел:
в виде двух чисел: 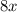 и
и 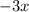 . А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.
. А затем сгрупируем по два члена в скобки и вынесен за скобки общий множитель.
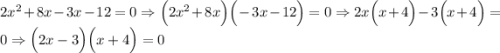
По правилу если произведение равно нулю, то хотя бы один из данных множителей будет равняться нулю. Рассмотрим 2 единственных случая.
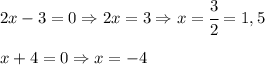
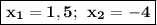 .Задание #7.
.Задание #7.Сделаем из данного уравнения систему и найдём дискриминант каждого нового уравнения. Если 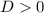 , то уравнение имеет 2 корня, если
, то уравнение имеет 2 корня, если 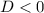 , то уравнение не имеет корней. (Если
, то уравнение не имеет корней. (Если 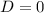 , то уравнение имеет 1 корень)
, то уравнение имеет 1 корень)
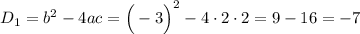
Т.к. 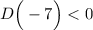 , то данное уравнение НЕ ИМЕЕТ КОРНЕЙ! Теперь находим дискриминант второго квадратного уравнения:
, то данное уравнение НЕ ИМЕЕТ КОРНЕЙ! Теперь находим дискриминант второго квадратного уравнения:
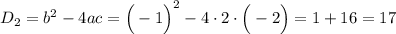
Т.к. 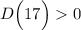 , то данное уравнение имеет 2 корня. Решим данное уравнение по формуле.
, то данное уравнение имеет 2 корня. Решим данное уравнение по формуле.
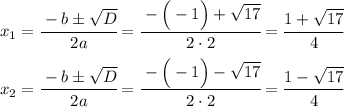
Сначала находим неизвестный множитель, деля произведение на известный множитель, а затем находим корень(-и) данного уравнения.
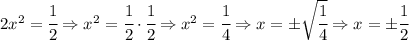
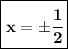
нахождение корней приведенного квадратного уравнения х²+3х+2=0 методом подбора, по теореме Виета
Используем формулы:
х₁+х₂=-p
x₁*x₂=q
х²+3х+2=0
p=3
q=2
x₁+x₂=-3 => x₁=--1; x₂=-2 -1+(-2)=-3
x₁*x₂=2 => x₁=-1; x₂=-2 (-1)*(-2)=2
нахождение корней с разложения квадратного трехчлена х²+3х+2=0 на множители
х²+3х+2 =
(х²+х)+(2х+2)= Теперь можно вынести общие множители за скобку
х(х+1)+(2(х+1)=
(х+2)(х+1)=0
Тогда:
или х+2=0 => x=-2
или х+1=0 => x=-1
x₁=-2
x₂=-1
решение квадратного уравнения через D (дискриминат) - дан в ответе другого пользователя.
Больший корень - х=-1, так как -2 < -1
ответ: х₁=-1; х₂-2