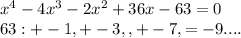
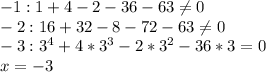
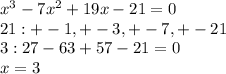
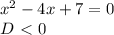
Для функции y(x)=x²-4x+3 найдите:
1 область определения функции;
2 множество значений функции;
3 наименьшее (наибольшее) значение функции;
4 уравнение оси симметрии параболы:
5 нули функции;
6 промежутки знакопостоянства функции;
7 промежутки монотонности функции
Объяснение:1. Область определения (-∞; +∞).
2. Область значений [-1; +∞).
3. Минимальное значение f(x) принимает в точке xmin = 2, f(2) = -1.
4. Ось симметрии x=2.
5. Нули функции x1=1, x2=3.
6. f(x)>0, при х∈(-∞;1)∪(3;+∞).
f(x)<0, при х∈(1;3).
7. f(x) убывает при х∈(-∞;2), f(x) возрастает при х∈(2;+∞).
Для функции y(x)=x²-4x+3 найдите:
1) область определения функции;
2)множество значений функции;
3)наименьшее (наибольшее) значение функции;
4)уравнение оси симметрии параболы:
5)нули функции;
6)промежутки знакопостоянства функции;
7)промежутки монотонности функции
X^4-3x^3-x^3+3x^2-5x^2+15x+21x-63=0
(X-3)(x^3-x^2-5x+21)=0
X1=3
X^3-x^2-5x+21=0
X^3+3x^2-4x^2-12x+7x+21=0
(X+3)(x^2-4x+7)=0
X2=-3
X^2-4x+7=0
D=4^2-4*1*7=16-28=-12<0
Это уравнение действительных корней не имеет.
Комплексные корни
X3=(4-i*√12)/2=2-i*√3
X4=2+i*√3