y=11+6√x-2x√x D(f)=x∈(0:+∞)
2x√x=2*x¹*x¹/₂=2*x³/²
6√x=6*x¹/²
f(x)=-2*x³/²+6*x¹/²+11
(2*x³/²)`=3*x¹/²=3√x
(6*x¹/²)`=3/x¹/²=3/√x
(11)`=0
f`(x)=-3√x+3/√x
Приравниваем производную к нулю:
-3√x+3/√x=0
-3√x*√х+3=0
-3х+3=0
-3х=-3
х=1 - критическая точка.
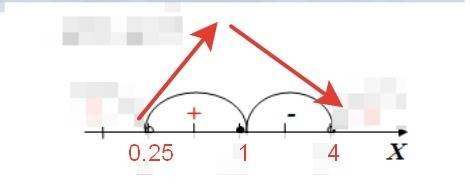
Чтобы узнать, достигает ли функция максимума в точке экстремума х=1, нужно определить знаки производной методом интервалов (рисунок во вложении):
f`(1)=0
f`(0.25)=-3√0.25+3/√0.25=4.5>0 - функция возрастает на отрезке (0;1)
f`(4)=-3√4+3/√4=-4.5<0 - функция убывает на отрезке (1;+∞)
При переходе через точку х=1 производная меняет знак с "+" на "-", значит х=1 - точка максимума функции.
По теореме Виета x1+x2=-2 (x1^+x2^+2x1x2)=4
2x1x2=0
4k^-60k+104=0
k^-15k+26=0
k1=13
k2=2
чтобы корни были действительными необходимо, чтобы
1-4k^+60k-104>=0
4k^-60k+103<=0
4*4-120+103=16-120+103<0 корень удовлетворяет
4*169-60*13+103=13(52-60)+103=103-13*8=103-104<0 корень подходит
k1=2
k2=13