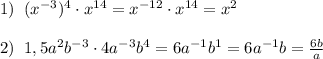
Пусть расстояние от города А до города В 1 (единица), х (ч) время за которое мотоциклист проехал расстояние от города А до города В, тогда по условию: х+3 (ч) время за которое пешеход от города А до города В (т.к. он вышел на 1 час раньше мотоциклиста из города А, но пришёл позже на 2 часа в город В. 1+2=3 (ч) разница) , 3-х (ч) время которое велосипедист был в пути, пока не начал движение мотоциклист из города А. Следовательно:
1÷х=1/х (рас/ч) скорость мотоциклиста.
1÷(х+30)=1/(х+3) (рас/ч) скорость пешехода.
(1/х)-(1/(х+3))=(х+3-х)/(х(х+3))=3/(х(х+3)) (рас/ч) скорость сближения мотоциклиста с пешеходом.
1*(1/(х+3))=1/(х+3) (км пешеход, пока не начал движение мотоциклист. (т.е. это расстояние между пешеходом и мотоциклистом, когда мотоциклист начал движение.)
1/(х+3)÷(3/(х(х+3))=1/(х+3)*(х(х+3))/3=х/3 (ч) время за которое мотоциклист проехал до встречи с пешеходом и велосипедистом.
(х/3)*(1/х)=1/3 (рас) от города А, где произошла встреча . (т.е. на расстоянии 1/3 от города А произошла встреча мотоциклиста с пешеходом и велосипедистом.)
1-(1/3)=2/3 (рас) проехал велосипедист от города В до встречи с пешеходом и мотоциклистом.
(3-х)+(х/3)=(9-3х+х)/3=(9-2х)/3 (ч) время, за которое велосипедист от города В проехал 2/3 пути до встречи.
((9-2х)/3)÷(2/3)=(9-2х)/2=4,5-х (ч) время, за которое велосипедист проехал весь путь, от города В до города А.
(4,5-х)-(3-х)=4,5-х-3+х=1,5 (ч). Через 1,5 часа после выезда мотоциклиста, велосипедист прибыл в город А.
Задача решена.
ответ: через 1,5 часа.
Д. - детский билет, В. - взрослый. Тогда:
2Д. + В. = 460 (1)
3Д. + 2В. = 795 (2)
Умножим обе части уравнения (1) на 2:
4Д. + 2В. = 920
Теперь вычтем из первого уравнения второе:
4Д. + 2В. - 3Д. - 2В. = 920 - 795
Д. = 125 (руб.) - подставим в (1):
В. = 460 - 250 = 210 (руб.)
Или так: Вычтем из уравнения (2) уравнение (1):
3Д. + 2В. - 2Д. - В. = 795 - 460
Д. + В. = 335 - стоимость одного детского и одного
взрослого билетов.
Д. = 335 - В. - подставим в (1):
2·(335 - В.) + В. = 460
В. = 670 - 460 = 210 (руб.)
Д. = 335 - 210 = 125 (руб.)