Объяснение:
Войти
РЕКЛАМА
Салют, Сбер! Переведи деньги
Делайте переводы голосом в моб приложении СберБанк Онлайн
Перейти
АнонимМатематика13 апреля 02:40
Теплоход проходит по течению реки до пункта назначения 76км и после стоянки возвращается в пункт отправления. Найдите
скорость теплохода в неподвижной воде, если скорость течения равна3 км/ч, стоянка длится 1 час, а в пункт отправления теплоход возвращается через 20 часов после отплытия из него.
РЕКЛАМА
Салют, Сбер! Переведи деньги
Делайте переводы голосом в моб приложении СберБанк Онлайн
Перейти
ответ или решение1
Яковлев Федор
Пусть собственная скорость теплохода х км/ч. Скорость теплохода по течению реки равна (х + 3) км/ч. Скорость теплохода против течения реки (х – 3) км/ч. На путь по течению реки теплоходу понадобилось 76/(х + 3) часа, а на путь против течения реки – 76/(х – 3) часа. На весь путь туда и обратно теплоход потратил (76/(х + 3) + 76/(х – 3)) часа или (20 – 1) = 19 часов. Составим уравнение и решим его.
76/(х + 3) + 76/(х – 3) = 19 – приведем к общему знаменателю (х + 3)(х – 3) = x^2 – 9; первую дробь домножим на (х – 3), вторую – на (х + 3) и число 19 – на (x^2 – 9); далее решаем без знаменателя, т.к. две дроби с одинаковым знаменателем равны, если равны их числители;
76(x – 3) + 76(x + 3) = 19(x^2 – 9);
76x – 228 + 76x + 228 = 19x^2 – 171;
-19x^2 + 76x + 76x + 171 = 0;
19x^2 – 152x – 171 = 0;
D = b^2 – 4ac;
D = (- 152)^2 – 4 * 19 * (- 171) = 23104 + 12996 = 36100; √D = 190;
x = (- b ± √D)/(2a);
x1 = (152 + 190)/(2 * 19) = 342/38 = 9 (км/ч);
x2 = (152 – 190)/(2 * 19) < 0 – скорость не может быть отрицательным числом.
ответ. 9 км/ч.
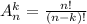
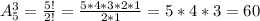
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-1)2 - 4·7·(-67) = 1 + 1876 = 1877
Z1 = 1 - √18772·7 ≈ -3.0232Z2 = 1 + √18772·7 ≈ 3.1660
Y^2=-100
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 02 - 4·1·100 = 0 - 400 = -400
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
5 = 15 x^2Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 02 - 4·15·(-5) = 0 + 300 = 300
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 0 - √3002·15 = -13√3 ≈ -0.5773502691896258
x2 = 0 + √3002·15 = 13√3 ≈ 0.5773502691896258
Z2 - 25 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 02 - 4·1·(-25) = 0 + 100 = 100
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 0 - √1002·1 = 0 - 102 = -102 = -5
x2 = 0 + √1002·1 = 0 + 102 = 102 = 5