x⁵+8x⁴+24x³+35x²+28x+12=0
Следствие из теоремы Безу гласит: "если многочлен с целыми коэффициентами имеет целый корень, то этот корень является делителем свободного члена".
Тогда корень данного уравнения находится среди делителей числа 12, то есть: ±1; ±2; ±3; ±4; ±6; ±12.
Подставляя значения в уравнения, получим, что x=-2 - корень уравнения.
Составим схему Горнера:
| 1 | 8 | 24 | 35 | 28 | 12 |
————————————
-2 | 1 | 6 | 12 | 11 | 6 | 0 |
Теперь можем разложить на множители исходное уравнение:
(x⁴+6x³+12x²+11x+6)(x+2)=0
Далее действия аналогичные:
Находим корень уравнения x⁴+6x³+12x²+11x+6=0 среди делителей его свободного члена: ±1; ±2; ±3; ±6.
Подставляя значения в уравнение x⁴+6x³+12x²+11x+6=0, получим, что x=-2 - корень уравнения.
Составляем схему Горнера:
| 1 | 6 | 12 | 11 | 6 |
—————————
-2 | 1 | 4 | 4 | 3 | 0 |
Теперь получим такое уравнение:
(x³+4x²+4x+3)(x+2)²=0
Находим корень уравнения x³+4x²+4x+3=0 среди делителей его свободного члена: ±1; ±3.
Подставляя значения в уравнение x³+4x²+4x+3=0, получим, что x=-3 - корень уравнения.
Составляем схему Горнера:
| 1 | 4 | 4 | 3 |
———————
-2 | 1 | 1 | 1 | 0 |
Получим такое уравнение:
(x²+x+1)(x+2)²(x+3)=0
x²+x+1=0 или (x+2)²=0 или x+3=0
∅ x=-2 x=-3
ответ: -3; -2.
Дана система уравнений:
{9x^2-42xy+52y^2-6y=265
{3x-7y-11=0.
Заданная система решается методом подстановки.
Из второго уравнения находим у = (3/7)х - (11/7) и подставляем вместо переменной у в первое уравнение.
Вычисление довольно громоздкое.
Результат: х1 = (-31/3), у1 = -6.
х2 = (67/3), у2 = 8.
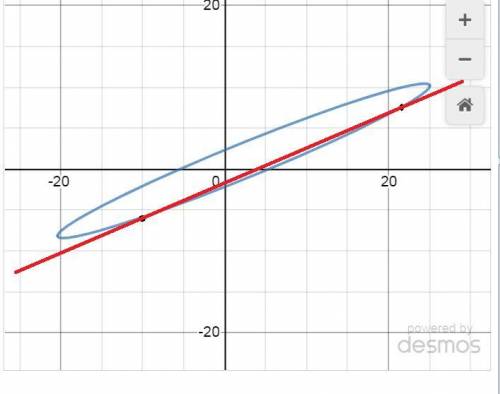
Первое уравнение - это эллипс, его уравнение линии 2-го порядка задано общим видом Ax² + 2Bx + Cy² + 2Dx + 2Ey + F = 0.
Продольная ось повёрнута от оси Ох на угол, определяемый по формуле tg(2α) = 2B/(A - C) = -42/(9 - 52) = 0,976744186 .
Угол поворота равен 22,163 градуса.
Угол наклона прямой, пересекающей эллипс равен arc tg(3/7) = 23,19859051 градуса.
Во вложении дан график эллипса и прямой.
x - 3y = -5
Ну, если надо не тупо решить, тогда сейчас попытаюсь объяснить.
У нас есть система из двух уравнений. Их можно сложить между собой. Но сделать это надо так, чтобы одно неизвестное пропало (или Х, или У). Для этого мы можем либо домножить первое уравнение на -1, тогда у нас пропадёт Х при сложении, либо второе домножить на -1, тогда тоже Х пропадёт, либо домножить первое на 3, тогда пропадёт У, или домножить второе на 1/3, тогда тоже У пропадёт.
Домножим второе уравнение на -1. Как это будет выглядеть:
x + y = 7
x - 3y = -5 | * (-1)
x + y = 7
-x + 3y = 5
Теперь мы можем сложить эти два уравнения.
x + (-x) + y + 3y = 7 + 5
И теперь решаем это уравнение:
x - x + y + 3y = 7 + 5
4y = 12
y = 12 : 4
y = 3
У нас есть У. Теперь его нужно подставить в любое уравнение (или первое, или второе). Проще это будет сделать, подставив в первое:
x + y = 7
x + 3 = 7
И решаем:
x = 7 - 3
x = 4
ответ: x = 4; y = 3.
Ещё ответ можно записать так: (4;3)