Найдите область определения функции а) у=2х²+3х-1 б) у=-х²+7х+2 в) у=√10-х(всё выражение под корнем) г) √х-11(всё выражение под корнем) д) у=2х+3/2-х е) у=7х+10/х+1

👇

Увидеть ответ

Ответ:

мам65

15.06.2021

а) любое икс;

б) любое икс;

в) 10-х не равно 0, т.е икс не равно 10;

г) икс не равно 11;

д) икс не равно 2;

е) икс не равно -1. Удачи!

4,6(74 оценок)

Открыть все ответы

Ответ:

anelya1429

15.06.2021

На графике функции 1) y = ½x³ лежат точки: A и C

На графике функции 2) y = -½x³ лежат точки: B и D

Объяснение:

Чтобы узнать, лежит ли точка на графике функции, достаточно подставить координаты точки в уравнение графика и проверить чему оно равно.

Например:

Чтобы проверить лежит ли точка А(2; 4) на графике функции y=½x³; подставим вместо переменной x координату x точки А (2), и если при этом выражение будет равно координате y точки A (4), то точка лежит на графике функции.

Первое число в скобках после наименования точки указывает на координату точки на оси X, второе число указывает на координату по оси Y. A (2;4) 2 - координата точки на оси X, 4 - координата точки на оси Y.

1) A (2;4)

Для графика функции y = ½x³:

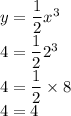
$y = \dfrac{1}{2} {x}^{3} \\ 4 = \dfrac{1}{2} {2}^{3} \\ 4 = \dfrac{1}{2} \times 8 \\ 4 = 4$

Верно, значит точка A лежит на графике функции y = ½x³

Для графика функции y = -½x³:

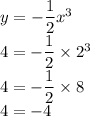
$y = - \dfrac{1}{2} {x}^{3} \\ 4 = - \dfrac{1}{2} \times {2}^{3} \\ 4 = - \dfrac{1}{2} \times 8 \\ 4 = - 4$

Неверно, значит точка A не лежит на графике функции y = -½x³.

2) B (-2;4)

Для графика функции y = ½x³:

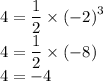
$4 = \dfrac{1}{2} \times { (- 2)}^{3} \\ 4 = \dfrac{1}{2} \times ( - 8) \\ 4 = - 4$

Неверно, значит точка B не лежит на графике функции y = ½x³.

Для графика функции y = -½x³:

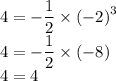
$4 = - \dfrac{1}{2} \times {( - 2)}^{3} \\ 4 = - \dfrac{1}{2} \times ( - 8) \\ 4 = 4$

Верно, значит точка B лежит на графике функции y = -½x³.

3) C (-2;-4)

Для графика функции y = ½x³:

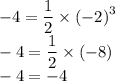
$- 4 = \dfrac{1}{2} \times {( - 2)}^{3} \\ - 4 = \dfrac{1}{2} \times ( - 8) \\ - 4 = - 4$

Верно, значит точка C лежит на графике функции y = ½x³.

Для графика функции y = -½x³:

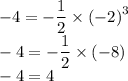
$- 4 = - \dfrac{1}{2} \times {( - 2)}^{3} \\ - 4 = - \dfrac{1}{2} \times ( - 8) \\ - 4 = 4$

Неверно, значит точка C не лежит на графике функции y = -½x³.

4) D (2;-4)

Для графика функции y = ½x³:

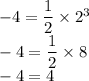
$- 4 = \dfrac{1}{2} \times {2}^{3} \\ - 4 = \dfrac{1}{2} \times 8 \\ - 4 = 4$

Неверно, значит точка D не лежит на графике функции y = ½x³.

Для графика функции y = -½x³:

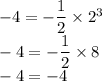
$- 4 = - \dfrac{1}{2} \times {2}^{3} \\ - 4 = - \dfrac{1}{2} \times 8 \\ - 4 = - 4$

Верно, значит точка D лежит на графике функции y = -½x³.

4,5(11 оценок)

Ответ:

0Али2005

15.06.2021

Расстояния:

от точки A до координатной плоскости

1) xy = 4

2) xz = 2

3) yz = 1

Объяснение:

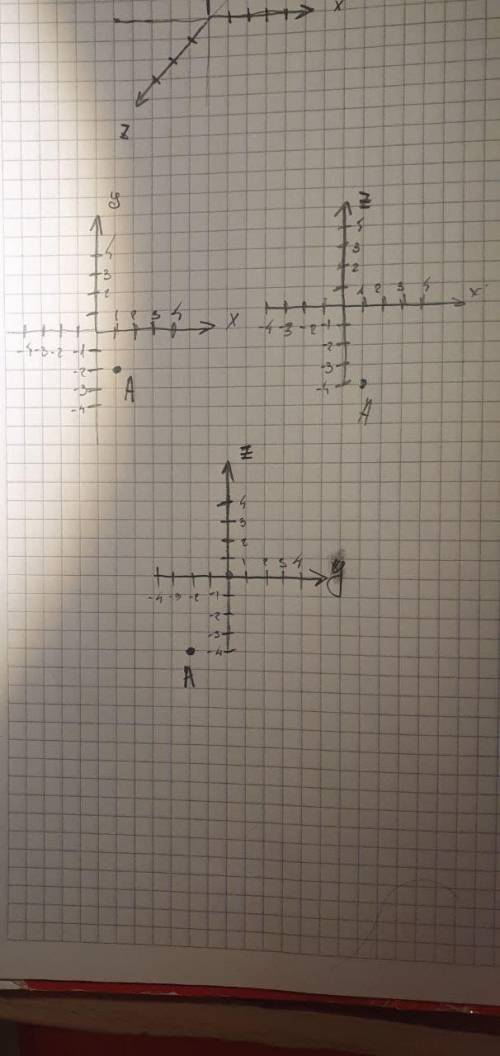
Для начала изображение. Очень сложно изобразить точку в трехмерном пространстве на бумаге, поэтому я нарисовал точку на 3-х плоскостях (xy, xz, yz)

Теперь найдем растояние точки от каждой плоскости. Пусть надо найти расстояние от точки A до плоскости xy. То есть x и y у нас те же а z=0.

Что это значит?

Вспомним формулу расстояния точки А(x1, y1, z1) до точки B (x2, y2, z2)

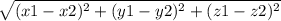
$\sqrt{(x1 - x2)^{2} + (y1 - y2)^{2} + (z1 - z2)^{2} }$

в нашем примере получается что x1 = x2 и y1 = y2. А что получается когда у нас 2 числа при отнимании равны? 0! А z2 у нас 0. Как я объяснял еще раньше.

поэтому функция иммет вид

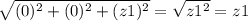
$\sqrt{(0)^{2} + (0)^{2} + (z1)^{2} }= \sqrt{z1^{2} }= z1$