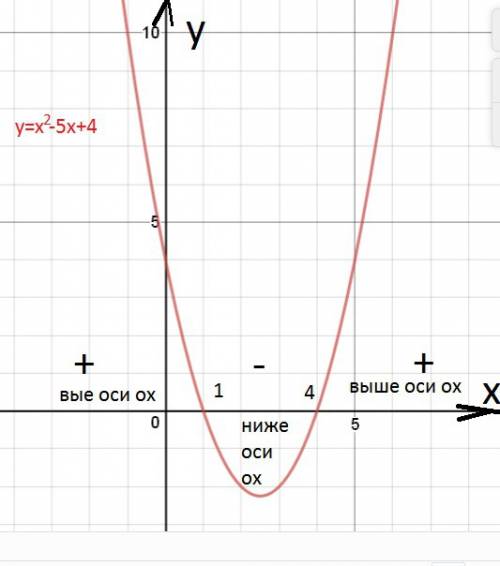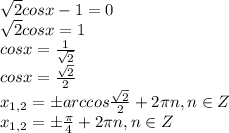
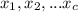 }. Возьмём произвольное число y, для которого выигрывает первый игрок. Понятно, что должно существовать такое z, что
}. Возьмём произвольное число y, для которого выигрывает первый игрок. Понятно, что должно существовать такое z, что 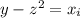 для некоторого i. То есть утверждение задачи эквивалентно тому, что существует некоторое конечное множество A такое, что любое натурально число либо принадлежит A, либо может быть представлено как
для некоторого i. То есть утверждение задачи эквивалентно тому, что существует некоторое конечное множество A такое, что любое натурально число либо принадлежит A, либо может быть представлено как 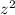 + элемент из А. (z - натуральное). Предположим, что это так. Тогда возьмём отрезок [1, m]. Далее будем брать элемент из A и прибавлять к нему квадраты натуральных чисел (1, 4, 9 ...) и если это число лежит в промежутке [1, m] увеличивать некий счётчик count. Понятно, что для элемента xi мы увеличим счётчик на
+ элемент из А. (z - натуральное). Предположим, что это так. Тогда возьмём отрезок [1, m]. Далее будем брать элемент из A и прибавлять к нему квадраты натуральных чисел (1, 4, 9 ...) и если это число лежит в промежутке [1, m] увеличивать некий счётчик count. Понятно, что для элемента xi мы увеличим счётчик на 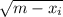 . Но тогда когда мы сделаем это для каждого элемента из A, в счётчике будет
. Но тогда когда мы сделаем это для каждого элемента из A, в счётчике будет ![[\sqrt{m - a_1}] + [\sqrt{m - a_2}] + ... + [\sqrt{m - a_c}] \ \textless \ = [\sqrt{m}] + ... + [\sqrt{m}] =](/tpl/images/0581/9108/146b0.png)
![c[\sqrt{m}] \leq c\sqrt{m}](/tpl/images/0581/9108/2a2f9.png) , но так как m растёт быстрее, чем
, но так как m растёт быстрее, чем 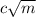 , то для некоторого m в промежутке [1...m] будут числа, не представимые в виде
, то для некоторого m в промежутке [1...m] будут числа, не представимые в виде 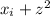 , приходим к противоречию, а значит утверждение задачи истинно. Замечание 1: понятно, что count >= чем чисел в промежутке [1, m], которые представимы как xi^2 + z^2. Замечание 2: [x] - целая часть числа х (или наибольшее целое число, не превосходящее x).
, приходим к противоречию, а значит утверждение задачи истинно. Замечание 1: понятно, что count >= чем чисел в промежутке [1, m], которые представимы как xi^2 + z^2. Замечание 2: [x] - целая часть числа х (или наибольшее целое число, не превосходящее x).