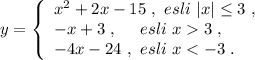
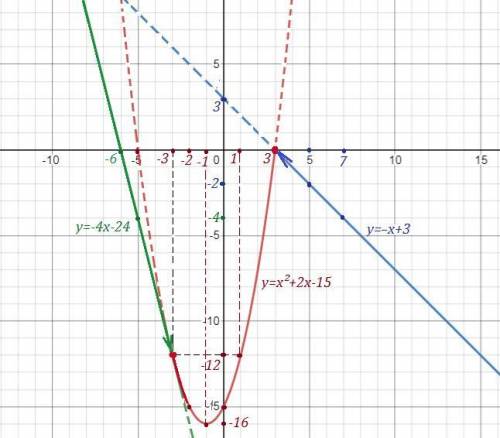
Кусочная функция на графике нарисована сплошными линиями .
Рисуем параболу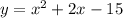 
при изменении переменной "х" в пределах от -3 до 3 , 
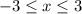. Ветви параболы направлены вверх, вершина параболы в точке (-1;-16) . Точки (3;0) и (-3;-12) принадлежат графику .
Прямую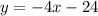 
рисуем при 
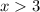. Точка (3;0) не принадлежит графику .
Прямую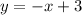 
рисуем при 
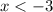. Точка (-3;-12) не принадле-жит графику .
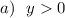при 
.
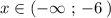б) область значений функции: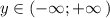 
,
при х=5 значение функции у=-2 ,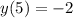 
.
в) пересечение с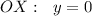 
при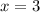 
, 
.
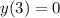пересечение с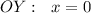 
, если 
.
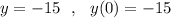г) y(x) возрастает при ![x\in [-1\ ;\ 3\ ]](/tpl/images/1787/8383/dc20e.png)
.
y(x) убывает при ![x\in (-\infty ;-1\ ]\cup [\ 3\ ;+\infty \, )](/tpl/images/1787/8383/485e8.png)
,
В решении.
Объяснение:
Чи належить графіку лінійного рівняння з двома змінними 7х+2у-3=0 точка:
1) А(2; -3)
2) В(3; -6)
3) С(-3; -2)
4) Д(0; 1)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение. Если левая часть равна правой, то принадлежит, и наоборот.
1) 7х+2у-3=0; А(2; -3);
7*2 + 2*(-3) - 3 = 14 - 6 - 3 = 5;
5 ≠ 0, не принадлежит.
2) 7х+2у-3=0; В(3; -6);
7*3 + 2*(-6) - 3 = 21 - 12 - 3 = 6;
6 ≠ 0, не принадлежит;
3) 7х+2у-3=0; С(-3; -2);
7*(-3) + 2*(-2) - 3 = -21 - 4 - 3 = -28
-28 ≠ 0, не принадлежит;
4) 7х+2у-3=0; Д(0; 1);
7*0 + 2*1 - 3 = 0 + 2 - 3 = -1;
-1 ≠ 0, не принадлежит.
|b|- модуль b
sqrt(9x²-24x+16)=5
Под корнем можем собрать квадрат разности
sqrt((3x-4)²)=5
Корень квадрата это модуль этого числа
|3x-4|=5
Раскрываем модуль
3х-4=5 и 3х-4=-5
Дальше считаем
3х=9 и 3х=-1
х=3 и х=1/3 корни уравнения