ответ: 1-б. 2-а, 3-г, 4-, 5- , 6-в, 7-г
Объяснение:
1. Найдите значение алгебраической дроби 2х/х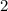
-1, при х= 1/3
• а) 0,75; б) -0,75 ; в) - ;г) -1,5
2. Найдите значение x, при котором дробь х+2/х-4 не имеет смысла
а)4 б)-2 в) -4 г) нет таких значений
3. Какое из предложенных выражений записано в виде алгебраической дроби?
а)2х/3+х ; б)2/х2+3х в)81х2/13-х ; г)2/3-х
4. Найдите значение выражения , при а= -0,7, в=0,3
а)2,5; б) -2,5; в) 1; г) другой ответ.
5.При каком значении а дробь не определена?
а) 0; б) - ; в) ; г)другой ответ.
6. Найди допустимые значения букв, входящих в дробь а/b
а) любые значения; б)5 возможных значений ; в) любые значения а и b, при b не равным 0 ; г) нет ответа
7.Выберите дробно- рациональные выражения 2х/3+4/7, 2-5х/7,3, 3/х-2
а) нет правильного ответа ; б) 2х/3+4/7 ; в)2-5х/7,3 ; г) 3/х-2
Решение.
Если у=х²-3х , то неравенство y<0 равносильно неравенству
х²-3х<0 . Решим его методом интервалов.
Разложим на множители левую часть неравенства, получим
х·(х-3)<0
Найдём нули функции (произведения), записанной в левой части неравенства. Это те значения х, при которых левая часть обращается в 0 . Это будет при х=0 или при х-3=0 , х=3.
Нанесём нули функции на числовую ось (0)(3)
и подсчитаем знаки функции на полученных интервалах .
Для этого берём какую-нибудь точку из интервала и считаем знак функции .
Пусть х= -10, тогда х·(х-3)= -10·(-10-3)= -10·(-13)>0 . Ставим знак (+) в левом интервале (-∞ ; 0 ) .
Пусть х= 1, тогда х·(х-3)=1·(1-3)=1·(-2)<0 . Ставим знак (-) в среднем интервале ( 0 ; 3 ) .
Пусть х= 10, тогда х·(х-3)=10·(10-3)=10·7>0 . Ставим знак (+) в правом интервале ( 3 ; +∞ ) .
Получили + + + (0) - - - (3) + + +
Так как задано неравенство со знаком < , то смотрим, в каком промежутке записан знак минус и пишем ответ.
ответ: х ∈ ( 0 ; 3 ) .
на фото...............