Пусть для определенности в каждом сосуде было по 1 л раствора, в котором x л кислоты. Тогда в 1 сосуде после 1 переливания будет
x*(1 - m)/1 л кислоты. А после 2 переливания будет
x*(1 - m)^2 л кислоты.
Точно также во 2 сосуде после 2 переливания будет
x*(1 - 2m)^2 л кислоты.
И по условию эти объемы относятся друг к другу как 26/16 = 13/8.
x*(1 - m)^2 : [x*(1 - 2m)^2] = 13/8
(1 - m)^2 : (1 - 2m)^2 = 13/8
8(1 - m)^2 = 13(1 - 2m)^2
После раскрытия квадратов получаем:
8m^2 - 16m + 8 = 52m^2 - 52m + 13
44m^2 - 36m + 5 = 0
D/4 = 18^2 - 44*5 = 324 - 220 = 104
m1 = (18 - √104)/44 ~ 0,1773; m2 = (18 + √104)/44 ~ 0,6408
Но во 2 случае объем 2m = 1,2816 > 1 л, поэтому не подходит.
ответ: 0,1773 часть объема раствора
Но мне кажется, что в задаче ошибка, должно быть 25/16.
Тогда решение намного проще.
(1 - m)^2 : (1 - 2m)^2 = 25/16
(1 - m) : (1 - 2m) = 5/4
4(1 - m) = 5(1 - 2m)
4 - 4m = 5 - 10m
6m = 1
m = 1/6 часть объема раствора
Объяснение:
Задание 2.
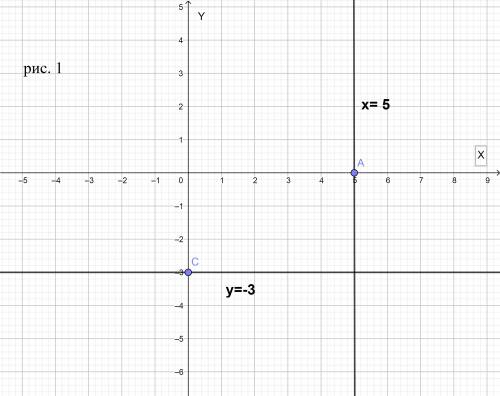
а) Координату х=5 будут иметь все точки , лежащие на прямой , которая параллельна оси ординат и проходит через т.А на оси абсцисс. Любая другая точка координатной плоскости имеет абсциссу отличную от х=5
б) Координату у=-3 будут иметь все точки , лежащие на прямой , которая параллельна оси абсцисс и проходит через т.С на оси ординат. Любая другая точка координатной плоскости имеет ординату отличную от у=-3
рисунок 1 во вложении
Задание 3.
а) На координатной плоскости неравенство х ≥ 4 задаст полуплоскость , которая будет расположена правее прямой х=4. Все точки этой полуплоскости будут иметь абсциссу равную 4 и больше
рисунок 2 во вложении
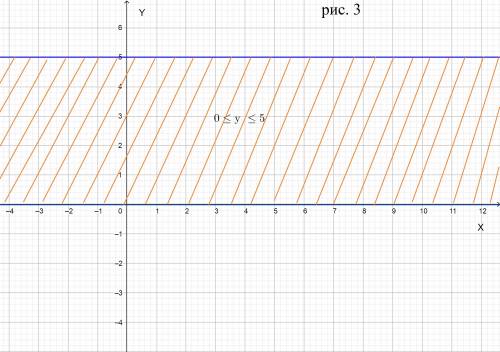
б) Двойное неравенство 0 ≤ у ≤ 5 задает на координатной плоскости две горизонтальные полосы , которые имееют ординату 0 и 5
рисунок 3 во вложении
Задание 4.
а) у = х;
найдем точки и построим график
х=0, у=0
х=3 , у=3
х=-3, у= -3
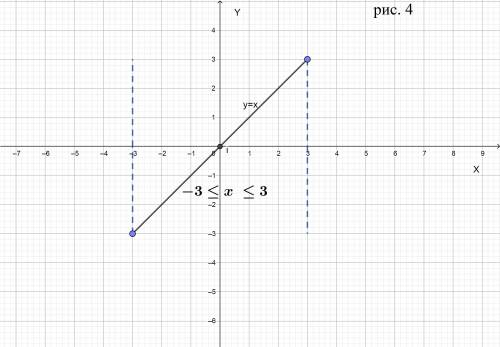
б) –3 ≤ х ≤ 3.
неравенство задает на координатной плоскости две вертикальные полосы, которые имею абсциссу 3 и -3
Изобразим множество точек на координатной плоскости
рисунок 4 во вложении
Задание 5
Решение во вложении
Задание 6
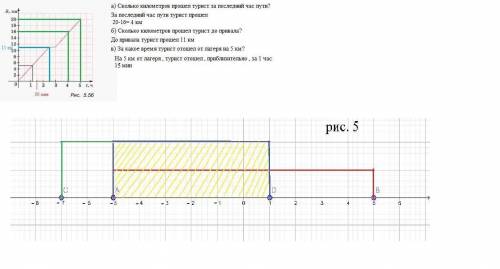
Если | x | ≤ 5 , значит -5 ≤ х ≤ 5, т.е. х ϵ [-5 ; 5]
Отметим этот промежуток т.А и т.В на координатной прямой ( рис. 5 во вложении)
Отметим промежуток –7 ≤ x ≤ 1 , т.е. х ϵ [ -7 ; 1] на координатной прямой т.С и т. D
Для того, чтобы определить границы промежутков [-5; 5] и [-7; 1] сравним левые и правые границы этих промежутков. Поскольку -7 < -5, а 5 >1 , то искомое пересечение имеет вид: х ϵ[-5; 1]

Уравнение плоскости XOY: z=0
Уравнение плоскости YOZ: x=0
Уравнение плоскости XOZ: y=0
D(-4;-2;1)
Расстояние от точки до плоскости равно:
Находим расстояние до XOY:
A=0
B=0
C=1
D=0
До XOZ:
A=0
B=1
C=0
D=0
До YOZ:
A=1
B=0
C=0
D=0