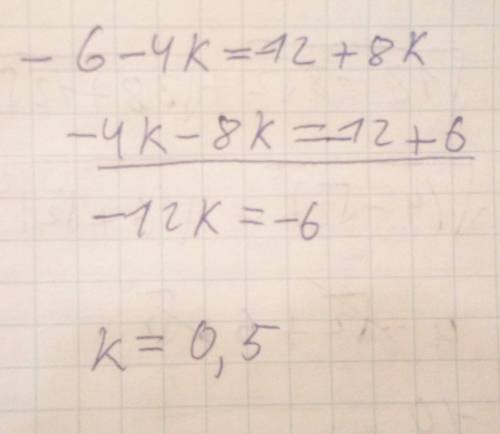
Задача. Катер плыл по течению реки 4 часа , а против течения 5 часов. Расстояние, которое катер проплыл туда и обратно равно 114 км . Найти собственную скорость катера, если скорость течения реки равно 3 км/час .
Решение. Собственная скорость катера равна х км/ч.
По течению реки его скорость равна (х+3) км/ч и проплыл он 4(х+3) км .
Против течения реки скорость катера равна (х-3) км/ч и проплыл он 5(х-3) км .
Всего катер проплыл 114 км. Составим уравнение:
4(х+3)+5(х-3)=114
4x+12+6x-15=114
10x=117
x=11,7
ответ: скорость катера равна 11,7 км/ч .
1/x-1/y=1/6
6y/6xy-6x/6xy=xy (приводим к общему знаменателю)
6y-6x=xy
6(y-x)=xy
Это мы упростили первое уравнение
Второе:
xy(y-x)=6 (вынесли ху за скобку)
Подставляем первое уравнение во второе
6(y-x)(y-x)=6
(y-x)^2=1 (^2 - значит в квадрате)
y-x=1
y=x+1
Подставляем это вместо xy(y-x)=6
x(x+1)(x+1-x)=6
x^2+x=6 т.к во второй скобке +х и -х сокращаются и остается 1.
x^2+x-6=0
Решаем через дискриминант
D=25
x1=(-1+5)/2=2 > y1=2+1=3
x2=(-1-5)/2=-3 > y2=-3+1=-2
ответ: (2,3),(-3,-2)
По всем вопросам пишите в личку
-12k=-6
все делим на -12
k=0,5