logo
Вход Регистрация Спроси Mozg AI
М
Молодежь
К
Компьютеры-и-электроника
Д
Дом-и-сад
С
Стиль-и-уход-за-собой
П
Праздники-и-традиции
Т
Транспорт
П
Путешествия
С
Семейная-жизнь
Ф
Философия-и-религия
Б
Без категории
М
Мир-работы
Х
Хобби-и-рукоделие
И
Искусство-и-развлечения
В
Взаимоотношения
З
Здоровье
К
Кулинария-и-гостеприимство
Ф
Финансы-и-бизнес
П
Питомцы-и-животные
О
Образование
О
Образование-и-коммуникации
тик12345
тик12345
27.05.2020 16:00 •  Алгебра

Сократите дробь: 3 в степени n-1 умноженное на 5 в степени 2n-1 делить на 75 в степени n

👇
Увидеть ответ
Ответ:
1mizik1
1mizik1
27.05.2020

\frac{3^{n-1}\cdot5^{2n-1}}{75^n}=\frac{3^{n-1}\cdot5^{2n-1}}{(3\cdot5^2)^n}=\frac{3^{n-1}\cdot5^{2n-1}}{3^n\cdot5^{2n}}=3^{n-1-n}\cdot5^{2n-1-2n}=3^{-1}\cdot5^{-1}=\frac{1}{3\cdot5}=\frac{1}{15}

4,4(15 оценок)
Открыть все ответы
Ответ:
den4ik143
den4ik143
27.05.2020
Наклонной асимптотой и касательной является прямая вида:
у=kх+b, где k-угловой коэффициент прямой.
Геометрический смысл производной:
k=tgα=f '(x₀) 
чтобы прямые были параллельными, необходимо и достаточно, чтобы соответственные углы были равны, то есть:
α=β ⇒ tgα=tgβ ⇒ k₁=k₂

если функция задаётся дробью в которой в числителе и знаменателе стоят многочлены, то наклонную асимптоту можно найти делением числителя на знаменатель столбиком и то что получится в частном и будет наклонная асимптота (см.фото 1) у=kx+b
y=x+2 ⇒ k₁=1
или в общем виде найти через предел (см. фото 2)

y= \sqrt{x} \\ y'= \frac{1}{2 \sqrt{x_0} } = \frac{1}{2 \sqrt{0.25} } = \frac{1}{2*0.5}=1 \\ y'=tg \ \beta =k _2 \\ k_2=1 \\

Итак, k₁=k₂=1, следовательно данные наклонная асимптота и касательная параллельны - ч.т.д
Докажите, что наклонная асимптота графика функции параллельна касательной к графику в точке с абцисс
Докажите, что наклонная асимптота графика функции параллельна касательной к графику в точке с абцисс
4,7(80 оценок)
Ответ:
LoveSmile78900987
LoveSmile78900987
27.05.2020

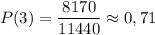
а) 8170

б) ≈ 0,71

Объяснение:

а)

Количество выбора m элементов из n - это число сочетаний из n по m:

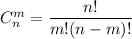
C_n^m=\dfrac{n!}{m!(n-m)!}

Девочек должно быть не меньше трех. Значит возможны варианты выбора семи школьников в комитет:

3 девочки из семи и 4 мальчика из девяти (применяем правило произведения):

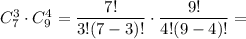
C_7^3\cdot C_9^4=\dfrac{7!}{3!(7-3)!}\cdot \dfrac{9!}{4!(9-4)!}=

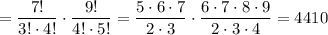
=\dfrac{7!}{3!\cdot 4!}\cdot \dfrac{9!}{4!\cdot 5!}=\dfrac{5\cdot 6\cdot 7}{2\cdot 3}\cdot \dfrac{6\cdot 7\cdot 8\cdot 9}{2\cdot 3\cdot 4}=4410

4 девочки и 3 мальчика:

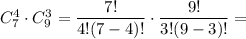
C_7^4\cdot C_9^3=\dfrac{7!}{4!(7-4)!}\cdot \dfrac{9!}{3!(9-3)!}=

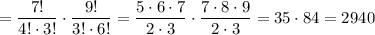
=\dfrac{7!}{4!\cdot 3!}\cdot \dfrac{9!}{3!\cdot 6!}=\dfrac{5\cdot 6\cdot 7}{2\cdot 3}\cdot \dfrac{7\cdot 8\cdot 9}{2\cdot 3}=35\cdot 84=2940

5 девочек и 2 мальчика:

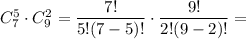
C_7^5\cdot C_9^2=\dfrac{7!}{5!(7-5)!}\cdot \dfrac{9!}{2!(9-2)!}=

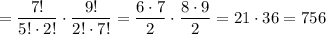
=\dfrac{7!}{5!\cdot 2!}\cdot \dfrac{9!}{2!\cdot 7!}=\dfrac{6\cdot 7}{2}\cdot \dfrac{8\cdot 9}{2}=21\cdot 36=756

6 девочек и 1 мальчик:

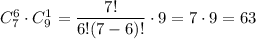
C_7^6\cdot C_9^1=\dfrac{7!}{6!(7-6)!}\cdot 9=7\cdot 9=63

и, наконец, все 7 человек - девочки .

По правилу суммы:

4410 + 2940 + 756 + 63 + 1 = 8170 - количество выбрать 7 человек в комитет так, чтобы в нем было не менее трех девочек.

б)

Всего школьников: 9 + 7 = 16 человек.

Количество выбрать 7 человек из шестнадцати:

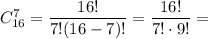
C_{16}^7=\dfrac{16!}{7!(16-7)!}=\dfrac{16!}{7!\cdot 9!}=

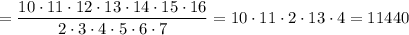
=\dfrac{10\cdot 11\cdot 12\cdot 13\cdot 14\cdot 15\cdot 16}{2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7}=10\cdot 11\cdot 2\cdot 13\cdot 4=11440

Вероятность того, что в комитете будет не менее трех девочек:

P(3)=\dfrac{8170}{11440}\approx 0,71

4,8(95 оценок)
Это интересно:
О
Как нарисовать банан: подробная инструкция для начинающих...
С
Правильный выбор парика: все, что вам нужно знать...
К
Как удалить историю поиска в iPod Touch: шаги по настройке конфиденциальности...
З
Здоровье
10.07.2021
Голубые глаза: миф или реальность?...
О
Как убедить человека рассказать свой секрет? Открываем профессиональные секреты психологии...
Х
Как выбрать апертуру объектива: все, что вам нужно знать...
К
Как исправить проблемы с завершением работы Windows...
К
Как приготовить тыкву: от супа до печенья...
П
Как завоевать доверие собаки: советы для новичков...
Х
Как использовать объективы с байонетом M42 на цифровых фотоаппаратах Canon EOS...
Новые ответы от MOGZ: Алгебра
I3eTePo4eK265
I3eTePo4eK265
30.07.2022
Представьте выражение 1/x^-6*1/x^9 в виде степени с основанием x...
lerkakotik1983
lerkakotik1983
30.07.2022
Первоначально футболка стоила 320 рублей . на распродаже ее цена снизилась на 15%. сколько рублей стала стоить футболка после скидки ?...
Bakc1
Bakc1
30.07.2022
Диаметры двух деревянных шаров,изготовленных из дуба и сосны,одинаковы.что можно сказать о массах этих шаров? 1)масса дубового шара больше,чем соснового. 2)масса соснового...
nikop65
nikop65
02.01.2020
Площадь поверхности урана – одной из планет солнечной системы – равна 8120 млн км². как эта величина записывается в стандартном виде? 1)8,120 * 109 км22)8,120 * 108 км23)8,120...
oliesiaolieska
oliesiaolieska
02.01.2020
Какое из уравнений имеет два различных корня 1) x^2 - 2x + 5 = 0 2) 9x^2 - 6x + 1 = 0 3) 2x^2 - 7x + 2 = 0 4) 3x^2 - 2x + 2 = 0...
Mamayuliya1986
Mamayuliya1986
02.01.2020
Какое из следующих утверждений верно? 1)основания равнобедренной трапеции равны 2)центр описанной около треугольника окружности всегда лежит внутри этого треугольника 3)все...
qwertyuiop314
qwertyuiop314
02.01.2020
Решите уравнение (x−3)^2(x−5)=35(x−3)....
Шkolnitsa
Шkolnitsa
02.01.2020
Преобразуйте выражение в многое стандартного вида а) -5an(3a2-0,2b+ab б)(a+4)(a-5) в)(35a3b-28a4): 7a3...
OToMCTuTEL
OToMCTuTEL
02.01.2020
Как найти корни уравнения такого типа: (x+8)^2=(x+3)^2 формулу видел к типа ax^2+bx+c...
arujan20071
arujan20071
02.01.2020
Уменя лёгкие и смешные примеры! 1.можно ли к рациональному числу прибавить иррациональное,например 5√3 + 2 будет 7√3 или ни в коем случае нельзя так делать? 5√3 -2? 2.а если...

MOGZ ответил

Полный доступ к MOGZ
Живи умнее Безлимитный доступ к MOGZ Оформи подписку
О НАС
ПОМОЩЬ
App
.
.
logo
Вход Регистрация
Что ты хочешь узнать?
Спроси Mozg
Открыть лучший ответ