Рациональные дроби" 7 класс
Дробно-рациональное выражение — это дробь, числителем и знаменателем которой являются многочлены с рациональными(целыми) коэффициентами. Она имеет вид
где P(x) и Q(x) некоторые многочлены.
Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.
Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби
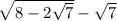
тут мы иммем дело с разницей квадрата под корнем. его надо уметь видеть.
= 
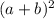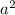+ 2ab +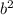 
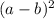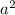= - 2ab +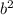
в данном случе второе(минус перед два корней из семи).
И так 2√7 - в данном случае это у нас 2ab.
8 - это сума а в квадрате и б в квадрате.
то есть:
8 = +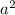
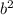
2ab = 2√7
ab = √7
То есть нам нужно методом подбора подобрать такие числа, чтобы их сумма в квадрате была 8, а при умножении они давали корень из семи. (тут метод подбора ничего более просто нужны тренировки и практика для этого).
Я подобрала:
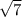и 1. И в правду, 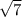* 1 =[/tex]\sqrt{7}[/tex]
и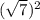 
+ 
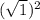= 7 + 1 = 8
то есть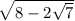 
= 
= |
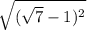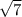- 1| (по модулю, модуль убираем, ибо 
|
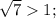То есть:
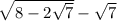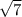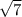= - 1 - = -1.
ответ: -1.
т.к. сумма всех углов треугольника равна 180° ⇒
∠В=180-50-60=70°
⇒
т.к. ∠В=∠В1=70° и ∠С=∠С1=60°
то треугольники подобны по двум углам (по 1 признаку)