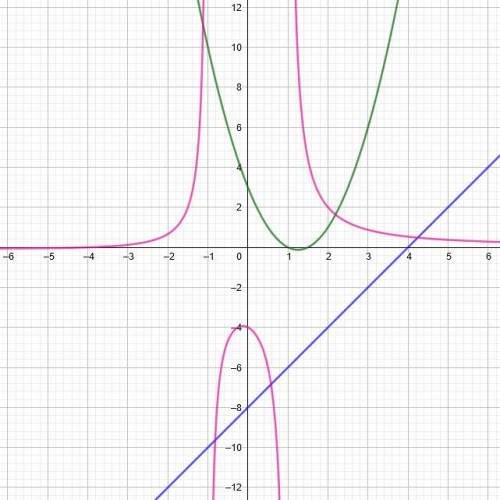
Тільки по графіку можна одразу вказати, при яких значеннях аргументу значення функції додатні
Приклад: Використовуючи графік функції у = х2 – 1, де -3 ≤ х ≤ 2, знайти значення аргументу, при яких функція набуває додатних значень;
Для значень х таких, що -3 < х < -1, точки графіка розташовані вище осі абсцис. Тому функція набуває додатних значень при -3 < х < -1. Так само вище осі абсцис знаходяться точки графіка для 1 < х < 2. Тому при 1 < х < 2 функція знову набуває додатних значень. Отже, при -3 < х < -1 або 1 < х < 2 функція набуває додатних значень.
а).
Просто подставляем в уравнение, задающее функцию,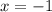 
:
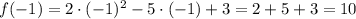
б).
Найдем те значения 
, при которых значение функции становится равным 
:
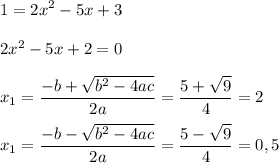
в).
Для того, чтобы определить, принадлежит ли точка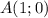 
графику, подставим в уравнение функци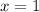и 
и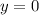 
, и посмотрим, что получится:
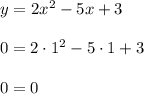
Получилось верное равенство! Значит, точка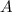 
действительно принадлежит графику рассматриваемой функции.
___________________________________________
Задание № 2.а).
Задача заключается в решении неравенства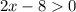 
:
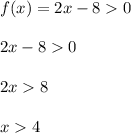
Получаем, что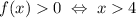 
, или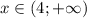 
.
б).
Ноли функции - это те значения , при которых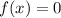 
:
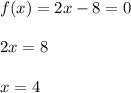
Значит, единственный ноль функции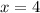 
.
___________________________________________
Задание № 3.а).
Область определения функции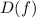 
- это те значения , при которых функция существует.
А функция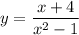 
существует только в том случае, если ее знаменатель не равен нолю:
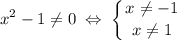
То есть, область определения данной функции - все действительные , кроме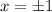 
:
Задача решена!
