

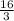
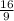
 или х₂ = 1
или х₂ = 1
1) Установить соответствие:
Угол ABC опирается на дугу ADC
Угол DEF опирается на дугу DCF
Угол AGF опирается на дугу ACF
2) Условно примем, что хорда АВ разделилась на отрезки АМ=25 см и ВМ=36 см. Тогда отношение частей хорды CD будет равно СМ/MD=1/4. Отрезки двух хорд связаны: произведение отрезков одной хорды равно произведению отрезков другой хорды.
Примем за х одну часть. Тогда СМ будет равен х, а MD - 4х. Составляем уравнение:
25*36=х*4х
900=4х^2
х^2=900/4
х^2=225
х=15
Находим 4х:
4*15=60 см.
Длина второй хорды равна 15+60=75 см. Следовательно, верный ответ 4 - 75 см.
3) Верный высказывания: 2 и 3.
Второе высказывание верно, потому что при делении числа на два не может быть двух разных результатов.
Третье высказывание верно, потому что градусная мера полуокружности равна 180 градусам, а вписанный угол равен половине градусной меры дуги, на которую опирается. Следовательно, вписанный угол, опирающийся на полуокружность, будет равен 180/2=90 градусов.
4) Определение вписанного угла: угол, стороны которого пересекают окружность, а вершина лежит на окружности, является вписанным. Следовательно, нужными пунктами будут 1 и 5.
5) Вписанными углами будут являться углы под номерами 1, 2 и 5.
6) Угол ABC - вписанный, значит градусная мера дуги, на которую он опирается, будет равна удвоенной градусной мере угла: 44*2=88 градусов.
Также указано, что дуга AB равна 92 градуса. Учитывая то, что вся окружность равняется 360 градусам, составляем уравнение:
Дуга BC=360-(88+92)
Дуга BC=360-180
Дуга ВС=180 градусов.
7) Из рисунка видно, что BC - это диаметр, следовательно, дуга BAC будет равна 180 градусов. Известно, что часть дуги ВАС - дуга ВА равна 100 градусам, значит вторая часть - дуга АС будет равна 180-100=80 градусов.
Угол ABC - вписанный, значит его градусная мера равна половине градусной меры дуги, на которую он опирается: 80/2=40 градусов.
8) Дуги АВ и ВС соприкасаются в точке В, значит дуга АВ+дуга ВС=дуга АВС; 152+80=232 градусов.
Дуга АС равна 360- 232= 128 градусов.
Угол AВС - вписанный, значит его градусная мера равна 128/2=64 градуса.
1) F(n) = 15^n + 13,
при n=1 получаем
15+13 = 28 кратно 7.
предположим, что выражение кратно 7 при любом натуральном k≤n, то есть, что
F(k) = 15^k + 13 = 7*A, где А - целое, k<=n,
тогда покажем, что это выражение F(k+1) также кратно 7.
F(k+1) = 15^(k+1) + 13 = 15*15^k + 13 = (14+1)*15^k + 13 = 14*(15^k) +
+ 15^k + 13 = 14*(15^k) + 7*A = 7*(2*15^k + A).
По методу мат. индукции мы доказали, что F(n) кратно 7 при любом натуральном n.
2) F(n) = 9^n + 5^n -2,
F(1) = 9 + 5 - 2 = 14 - 2 = 12 = 4*3, кратно 4.
Предположим, что для любого натурального k<=n F(k) кратно 4, то есть
F(k) = 9^k +5^k - 2 = 4*B,
Покажем тогда, что F(k+1) кратно 4:
F(k+1) = 9^(k+1) + 5^(k+1) - 2 = 9*(9^k) + 5*(5^k) - 2 = (8+1)*(9^k) +
+ (4+1)*(5^k) - 2 = 8*(9^k) + 9^k + 4*(5^k) + 5^k -2 =
= 8*(9^k) + 4*(5^k) + ( 9^k + 5^k - 2) = 8*(9^k) + 4*(5^k) + 4*B =
= 4*( 2*(9^k) + 5^k + B), последнее выражение в скобках очевидно целое, поэтому результат кратен 4.
3) F(n) = 5*(25^n) + 13*(13^(2n))
F(1) = 5*25 + 13*(13^2) = 125 + 13*169 = 125 + 2197 = 2322 = 9*258.
Предположим, что для любого k<=n F(k) кратно 9, то есть
F(k) = 5*(25^k) + 13*(13^(2k)) = 9*C,
тогда покажем, что F(k+1) кратно 9:
F(k+1) = 5*(25^(k+1)) + 13*( 13^(2*(k+1)) ) = 5*25*(25^k) + 13*(13^(2k+2)) =
= 5*25*(25^k) + 13*(13^2)*(13^(2k)) = 5*(27-2)*(25^k) + 13*(169)*(13^(2k)) =
= 5*27*(25^k) - 2*5*(25^k) + 13*(171-2)*(13^(2k)) =
= 5*27*(25^k) - 2*5*(25^k) + 13*171*(13^(2k)) - 2*13*(13^(2k)) =
= ( 5*27*(25^k) + 13*171*(13^(2k)) ) - 2*( 5*(25^k) + 13*(13^(2k)) ) =
= 9*( 5*3*(25^k) + 13*19*(13^(2k)) ) - 2*(9*C) =
= 9*( 5*3*(25^k) + 13*19*(13^(2k)) - 2*C ) и
F(k+1) кратно 9.
4) F(n) = 21^n + 4^(n+2)
F(1) = 21+ 4^3 = 21+64 = 85 = 17*5.
Предположим, что F(k) кратно 17 при любом натуральном k<=n, то есть
F(k) = 21^k + 4^(k+2) = 17*Q, где Q -целое,
Покажем тогда, что F(k+1) тоже кратно 17:
F(k+1) = 21^(k+1) + 4^( (k+1)+2 ) = 21*(21^k) + 4^(k+2+1) =
= (17+4)*(21^k) + 4*(4^(k+2)) = 17*(21^k) + 4*(21^k) + 4*(4^(k+2)) =
= 17*(21^k) + 4*( 21^k + 4^(k+2)) = 17*(21^k) + 4*17*Q =
= 17*( (21^k) + 4*Q ),
если k и Q - целые, то выражение в последних скобках тоже целое, и F(k+1) кратно 17.